VINS-MONO

Published: 2020-01-05 | Lastmod: 2020-03-03

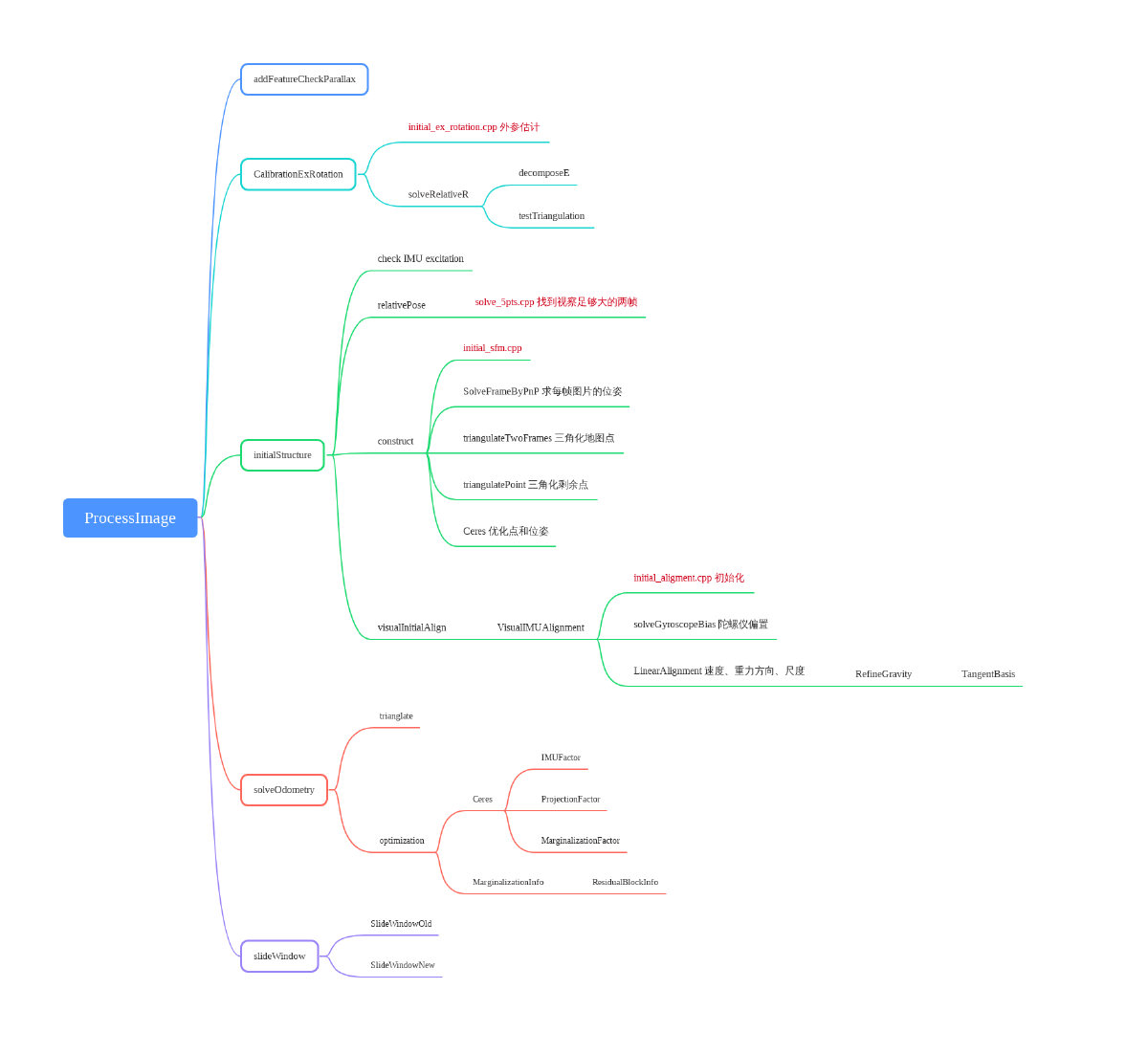
代码流程图 #

预积分的协方差 #

预积分值可以作为一种观测量，约束两个时刻状态间的关系。为了确定预积分值的精度（协方差），需要求解出其递推关系。

预积分公式推导

\(b_k^a\)和\(b_k^g\)作为随机游走噪声，在推导\(k \sim k+1\)时认为是常数！不像\(w\)和\(a\)，要添加\(n_k^g\)和\(n_k^a\)噪声进去

\[ \begin{aligned} \omega&=\frac{1}{2}( (\omega^{b_k}+n_k^g-b_k^g) + (\omega^{b_{k+1}}+n_{k+1}^g-b_k^g) ) \\[2mm] q_{b_ib_{k+1}}&=q_{b_ib_k}\otimes\begin{bmatrix}1 \\ \frac{1}{2}\omega\delta{t}\end{bmatrix} \\[2mm] a&=\frac{1}{2}( q_{b_ib_k}(a^{b_k}+n_k^a-b_k^a) + q_{b_ib_{k+1}}(a^{b_{k+1}}+n_{k+1}^a-b_k^a) ) \\[2mm] \beta_{b_ib_{k+1}}&=\beta_{b_ib_k}+a\delta{t} \\[2mm] \alpha_{b_ib_{k+1}}&=\alpha_{b_ib_k}+\beta_{b_ib_k}\delta{t}+\frac{1}{2}a\delta{t}^2 \\[2mm] b_{k+1}^a&=b_k^a+n_{b_k^a}\delta{t} \\[2mm] b_{k+1}^g&=b_k^g+n_{b_k^g}\delta{t} \\[2mm] \end{aligned} \]

写成矩阵形式：

\[ \begin{bmatrix}\alpha_{b_ib_{k+1}} \\ \theta_{b_ib_{k+1}} \\ \beta_{b_ib_{k+1}} \\ b_{k+1}^a \\ b_{k+1}^g\end{bmatrix} =F*\begin{bmatrix}\alpha_{b_ib_{k}} \\ \theta_{b_ib_{k}} \\ \beta_{b_ib_{k}} \\ b_{k}^a \\ b_{k}^g\end{bmatrix} +G*\begin{bmatrix}n_k^a \\ n_k^g \\ n_{k+1}^a \\ n_{k+1}^g \\ n_{k}^a \\ n_{k}^g \end{bmatrix} \]

\[ \begin{aligned} F&=\begin{bmatrix}I &f_{12} &I\delta{t} &-\frac{1}{4}(q_{b_ib_k}+q_{b_ib_{k+1}})\delta{t}^2 &f_{15}\\ 0 &I-[\omega]_{\times} &0 &0 &-I\delta{t}\\ 0 &f_{32} &I &-\frac{1}{2}(q_{b_ib_k}+q_{b_ib_{k+1}})\delta{t} &f_{35}\\ 0 &0 &0 &I &0\\ 0 &0 &0 &0 &I \end{bmatrix} \\[2mm] G&=\begin{bmatrix}\frac{1}{4}q_{b_ib_k}\delta{t}^2 &g_{12} &\frac{1}{4}q_{b_ib_{k+1}}\delta{t}^2 &g_{14} &0 &0 \\ 0 &\frac{1}{2}I\delta{t} &0 &\frac{1}{2}I\delta{t} &0 &0\\ \frac{1}{2}q_{b_ib_k}\delta{t} &g_{32} &\frac{1}{2}q_{b_ib_{k+1}}\delta{t} &g_{34} &0 &0\\ 0 &0 &0 &0 &I\delta{t} &0\\ 0 &0 &0 &0 &0 &I\delta{t}\end{bmatrix} \\[2mm] f_{12}&=-\frac{1}{4}( R_{b_ib_k}[a^{b_k}-b_k^a]_\times\delta{t}^2 + R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times(I-[\omega]_\times\delta{t})\delta{t}^2) \\[2mm] f_{32}&=-\frac{1}{2}( R_{b_ib_k}[a^{b_k}-b_k^a]_\times\delta{t} + R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times(I-[\omega]_\times\delta{t})\delta{t}) \\[2mm] f_{15}&=-\frac{1}{4}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t}^2)(-\delta{t}) \\[2mm] f_{35}&=-\frac{1}{2}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t})(-\delta{t}) \\[2mm] g_{12}&=g_{14}=-\frac{1}{4}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t}^2)(\frac{1}{2}\delta{t}) \\[2mm] g_{32}&=g_{34}=-\frac{1}{2}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t})(\frac{1}{2}\delta{t}) \end{aligned} \]

终极大矩阵

将所有值带进去并展开，得到原始等式

\[ \begin{aligned} q_{b_ib_{k+1}}&=q_{b_ib_k}\otimes\begin{bmatrix}1 \\ \frac{1}{2}\{\frac{1}{2}( (\omega^{b_k}+n_k^g-b_k^g) + (\omega^{b_{k+1}}+n_{k+1}^g-b_k^g) )\}\delta{t}\end{bmatrix} \\[2mm] \beta_{b_ib_{k+1}}&=\beta_{b_ib_k}+\{\frac{1}{2}( q_{b_ib_k}(a^{b_k}+n_k^a-b_k^a) + \{q_{b_ib_k}\otimes\begin{bmatrix}1 \\ \frac{1}{2}\{\frac{1}{2}( (\omega^{b_k}+n_k^g-b_k^g) + (\omega^{b_{k+1}}+n_{k+1}^g-b_k^g) )\}\delta{t}\end{bmatrix}\}(a^{b_{k+1}}+n_{k+1}^a-b_k^a) )\}\delta{t} \\[2mm] \alpha_{b_ib_{k+1}}&=\alpha_{b_ib_k}+\beta_{b_ib_k}\delta{t}+\frac{1}{2}\{\frac{1}{2}( q_{b_ib_k}(a^{b_k}+n_k^a-b_k^a) + \{q_{b_ib_k}\otimes\begin{bmatrix}1 \\ \frac{1}{2}\{\frac{1}{2}( (\omega^{b_k}+n_k^g-b_k^g) + (\omega^{b_{k+1}}+n_{k+1}^g-b_k^g) )\}\delta{t}\end{bmatrix}\}(a^{b_{k+1}}+n_{k+1}^a-b_k^a) )\}\delta{t}^2 \\[2mm] b_{k+1}^a&=b_k^a+n_{b_k^a}\delta{t} \\[2mm] b_{k+1}^g&=b_k^g+n_{b_k^g}\delta{t} \end{aligned} \]

矩阵形式

\[ \begin{aligned} \begin{bmatrix}\alpha_{b_ib_{k+1}} \\ \theta_{b_ib_{k+1}} \\ \beta_{b_ib_{k+1}} \\ b_{k+1}^a \\ b_{k+1}^g\end{bmatrix} &=\begin{bmatrix}I &-\frac{1}{4}( R_{b_ib_k}[a^{b_k}-b_k^a]_\times\delta{t}^2 + R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times(I-[\omega]_\times\delta{t})\delta{t}^2) &I\delta{t} &-\frac{1}{4}(q_{b_ib_k}+q_{b_ib_{k+1}})\delta{t}^2 &-\frac{1}{4}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t}^2)(-\delta{t})\\ 0 &I-[\omega]_{\times} &0 &0 &-I\delta{t}\\ 0 &-\frac{1}{2}( R_{b_ib_k}[a^{b_k}-b_k^a]_\times\delta{t} + R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times(I-[\omega]_\times\delta{t})\delta{t}) &I &-\frac{1}{2}(q_{b_ib_k}+q_{b_ib_{k+1}})\delta{t} &-\frac{1}{2}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t})(-\delta{t})\\ 0 &0 &0 &I &0\\ 0 &0 &0 &0 &I \end{bmatrix} *\begin{bmatrix}\alpha_{b_ib_{k}} \\ \theta_{b_ib_{k}} \\ \beta_{b_ib_{k}} \\ b_{k}^a \\ b_{k}^g\end{bmatrix}\\ &+\begin{bmatrix}\frac{1}{4}q_{b_ib_k}\delta{t}^2 &-\frac{1}{4}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t}^2)(\frac{1}{2}\delta{t}) &\frac{1}{4}q_{b_ib_{k+1}}\delta{t}^2 &-\frac{1}{4}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t}^2)(\frac{1}{2}\delta{t}) &0 &0 \\ 0 &\frac{1}{2}I\delta{t} &0 &\frac{1}{2}I\delta{t} &0 &0\\ \frac{1}{2}q_{b_ib_k}\delta{t} &-\frac{1}{2}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t})(\frac{1}{2}\delta{t}) &\frac{1}{2}q_{b_ib_{k+1}}\delta{t} &-\frac{1}{2}(R_{b_ib_{k+1}}[a^{b_{k+1}}-b_k^a]_\times\delta{t})(\frac{1}{2}\delta{t}) &0 &0\\ 0 &0 &0 &0 &I\delta{t} &0\\ 0 &0 &0 &0 &0 &I\delta{t}\end{bmatrix} *\begin{bmatrix}n_k^a \\ n_k^g \\ n_{k+1}^a \\ n_{k+1}^g \\ n_{k}^a \\ n_{k}^g \end{bmatrix} \end{aligned} \]

观测方程 #

观测方程，也就是状态量中的某种约束关系。一旦数学表达式列出来，求解就会顺其自然。

相机

观测方程：

\[ \begin{aligned} P_{w_l}&=R_{b_i}^w(R_c^b\frac{1}{\lambda_l}\pi_c^{-1}(\begin{bmatrix}\mu_l^{c_i}\\\nu_l^{c_i}\end{bmatrix})+p_c^b)+p_{b_i}^w \\[2mm] P_{w_l}&=R_{b_j}^w(R_c^bP_l^{c_j}+p_c^b)+p_{b_j}^w \\[2mm] P_l^{c_j}&=R_b^c\{R_w^{b_j}[R_{b_i}^w(R_c^b\frac{1}{\lambda_l}\overline{P}_l^{c_i}+p_c^b)+p_{b_i}^w-p_{b_j}^w]-p_c^b\} \end{aligned} \]

转换成矩阵形式：

\[ P_l^{c_j}=\begin{bmatrix} R_b^cR_w^{b_j} \\ -R_b^cR_w^{b_j}R_{b_i}^w(R_c^b\frac{1}{\lambda_l}\overline{P}_l^{c_i}+p_c^b)^{\wedge} \\ -R_b^cR_w^{b_j} \\ R_b^c\{R_w^{b_j}[R_{b_i}^w(R_c^b\frac{1}{\lambda_l}\overline{P}_l^{c_i}+p_c^b)+p_{b_i}^w-p_{b_j}^w]\}^\wedge \\ R_b^c(R_w^{b_j}R_{b_i}^w-I_{3\times3}) \\ -R_b^cR_w^{b_j}R_{b_i}^wR_c^b(\frac{1}{\lambda_l}\overline{P}_l^{c_i})^{\wedge}+(R_b^cR_w^{b_j}R_{b_i}^wR_c^b\frac{1}{\lambda_l}\overline{P}_l^{c_i})^{\wedge}+\{R_b^c[R_w^{b_j}(R_{b_i}^wp_c^b+p_{b_i}^w-p_{b_j}^w)-p_c^b]\}^{\wedge} \\ -R_b^cR_w^{b_j}R_{b_i}^wR_c^b\frac{1}{\lambda_l^2}\overline{P}_l^{c_i} \end{bmatrix}^T *\begin{bmatrix} p_{b_i}^w \\ q_{b_i}^w \\ p_{b_j}^w \\ q_{b_j}^w \\ p_c^b \\ q_c^b \\ \lambda_l \end{bmatrix} \]

IMU

观测方程：

\[ \gamma_B=\begin{bmatrix} R_w^{b_k}(p_{b_{k+1}}^w-p_{b_k}^w-\nu_{b_k}^w\Delta{t_k}+\frac{1}{2}g^w\Delta{t_k^2})-\alpha_{b_{k+1}}^{b_k} \\ 2[\gamma_{b_{k+1}}^{b_k}{\otimes}{q_{b_k}^w}^{-1}\otimes{q_{b_{k+1}}^w}] \\ R_w^{b_k}(\nu_{b_{k+1}}^w-\nu_{b_k}^w+g^w\Delta{t_k})-\beta_{b_{k+1}}^{b_k} \\ b_{a_{b_{k+1}}}-b_{a_{b_k}} \\ b_{\omega_{b_{k+1}}}-b_{\omega_{b_k}} \end{bmatrix} \]

转换成矩阵形式：

\[ \gamma_B=\begin{bmatrix} -R_w^{b_k} &0 &0 &0 &0 \\ [R_w^{b_k}(p_{b_{k+1}}^w-p_{b_k}^w-\nu_{b_k}^w\Delta{t_k}+\frac{1}{2}g^w\Delta{t_k^2})]^\wedge &-\mathcal{L}[{q_{b_{k+1}}^w}^{-1}\otimes{q_{b_k}^w}]\mathcal{R}[\gamma_{b_{k+1}}^{b_k}] &[R_w^{b_k}(\nu_{b_{k+1}}^w-\nu_{b_k}^w+g^w\Delta{t_k})]^\wedge &0 &0\\ -R_w^{b_k}\Delta{t} &0 &-R_w^{b_k} &0 &0\\ -\mathcal{J}_{b_a}^\alpha &0 &-\mathcal{J}_{b_a}^\beta &-I &0 \\ -\mathcal{J}_{b_\omega}^\alpha &-\mathcal{L}[{q_{b_{k+1}}^w}^{-1}\otimes{q_{b_k}^w}\otimes\gamma_{b_{k+1}}^{b_k}]\mathcal{J}_{b_\omega}^\gamma &-\mathcal{J}_{b_\omega}^\beta &0 &-I \\ R_w^{b_k} &0 &0 &0 &0 \\ 0 &\mathcal{L}[{\gamma_{b_{k+1}}^{b_k}}^{-1}\otimes{q_{b_{k}}^w}^{-1}\otimes{q_{b_{k+1}}^w}] &0 &0 &0\\ 0 &0 &R_w^{b_k} &0 &0\\ 0 &0 &0 &I &0\\ 0 &0 &0 &0 &I \end{bmatrix}^T *\begin{bmatrix} p_{b_k}^w \\ q_{b_k}^w \\ v_{b_k}^w \\ b_{a_k} \\ b_{\omega_k} \\ p_{b_{k+1}}^w \\ q_{b_{k+1}}^w \\ v_{b_{k+1}}^w \\ b_{a_{k+1}} \\ b_{\omega_{k+1}} \end{bmatrix} \]

在线标定 #

相机与IMU外参标定

利用对极几何原理，估算出连续两帧图像之间的旋转矩阵\(R\)，根据手眼标定公式：

\[ q_{b_k b_{k+1}} \otimes q_{bc} = q_{bc} \otimes q_{c_k c_{k+1}} \\[2mm] \left([q_{b_k b_{k+1}}]_L - [q_{c_k c_{k+1}}]_R\right)q_{bc}=Q^k_{k+1} \cdot q_{bc} = 0 \]

对应于CalibrationExRotation()函数，即可估算出相机与IMU外参。

想法： 这一步估算出来的外参精度应该并不高，因为两帧间的旋转矩阵精度不高，且会受到陀螺仪bias的影响。 这一部分误差将会被吸收到下一步的bias估计值中。

Bias估计

为了更精细的标定bias，需要采用SFM的方法：

1. relativePose 找到视察足够大的两帧，求解位姿
2. SolveFrameByPnP 求解每帧图片的位姿
3. triangulateTwoFrames 三角化地图点
4. triangulatePoint 三角化剩余点
5. Ceres 优化点和位姿

求解出所有图像帧的位姿，进行Bias估计：

\[ \arg \min_{\delta b_g} \sum_{k \in B} \| 2 \lfloor q_{c_0 b_{k+1}}^{-1} \otimes q_{c_0 b_k} \otimes q_{b_k b_{k+1}} \rfloor_{xyz} \|^2 \\[2mm] q_{b_k b_{k+1}} \approx \hat{q}_{b_k b_{k+1}} \otimes \begin{bmatrix} 1 \\ \frac{1}{2}J^q_{b_g} \delta b_g \end{bmatrix} \]

PVQ参数优化

P: 图像与IMU的位置对齐，仅缺少一个尺度s
V: 每帧图像时刻对应的IMU的速度
Q: 外参已对齐，缺少初始的绝对姿态，即初始重力的方向

预积分公式重温：

\[ \begin{aligned} p_{wb_j}&=p_{wb_i}+v_i^w\Delta t - \frac{1}{2}g^w\Delta t^2 + q_{wb_i}\int\int_{t\in[i,j]}(q_{b_i b_t}a^{b_t})\delta t^2 \\[2mm] v_j^w&=v_i^w - g^w\Delta t + q_{wb_i}\int_{t\in[i,j]}(q_{b_i b_t}a^{b_t})\delta t \\[2mm] q_{wb_j}&=q_{wb_i}\int_{t\in[i,j]}q_{b_i b_t}\otimes\begin{bmatrix}0 \\ \frac{1}{2}w^{b_t} \end{bmatrix} \delta t \end{aligned} \]

其中位置、速度的预积分中，包含了我们需要估计的所有参数。 以位置、速度的预积分作为观测值，列出如下方程：

\[ \begin{aligned} \begin{bmatrix} \alpha_{b_i b_j} \\ \beta_{b_i b_j} \end{bmatrix}= \begin{bmatrix} q_{b_i w}(p_{w b_j} - p_{w b_i} -v_i^w\Delta t + \frac{1}{2} g^w \Delta t^2) \\ q_{b_i w}(v_j^w - v_i^w + g^w \Delta t) \end{bmatrix}= H \cdot \begin{bmatrix} v_k^{b_k} \\ v_{k+1}^{b_{k+1}} \\ g^{c_0} \\ s\end{bmatrix} + n \end{aligned} \]

即可进行最小二乘求解了。

优化绝对位姿

对重力方向进行如下建模：

\[ \hat g^{c_0} = \|g\| \cdot \hat{\bar{g}}^{c_0} + w_1 \vec{b_1} + w_2 \vec{b_2} \]

重新进行优化，可以得到更精确的重力向量方向，即初始状态的绝对位姿。

求解 #

使方程满秩可求解

信息矩阵 \(H\) 不满秩

1. 用LM方法求解，会导致H满秩 --> 解在空间中整体变化
2. 添加先验约束，增加系统可观性。例如固定第一个相机，\(H_{[11]}+=I\)
3. 添加超强先验，使得对应的信息矩阵巨大\(H_{[11]}=\infty\)，就能使得\(\Delta{x}=H^{-1}b=0\)
4. 设定对应雅克比矩阵为 0，则\(H_{[11]}=0\)，\(b_{[1]}=0\)。则在求解时，\((0+\lambda{I})\Delta{x}=0\)

舒尔补

更新先验残差

舒尔补之后的状态量的雅克比不再更新，当状态更新时，残差值需要同步更新。

\[ \begin{aligned} b_p^{'}&=b_p+\frac{\partial{b_p}}{\partial{x_p}}\delta{x_p}\\ &=b_p+\frac{\partial{(-J^T\Sigma^{-1}r)}}{\partial{x_p}}\delta{x_p}\\ &=b_p-\Lambda_p\delta{x_p} \end{aligned} \]

Ceres在VINS-MONO中的使用 #

Ceres的具体用法，及其在VINS-MONO中的用法，请参考如下文章： non-linear

Next: 非线性优化
Previous: ORB-SLAM2