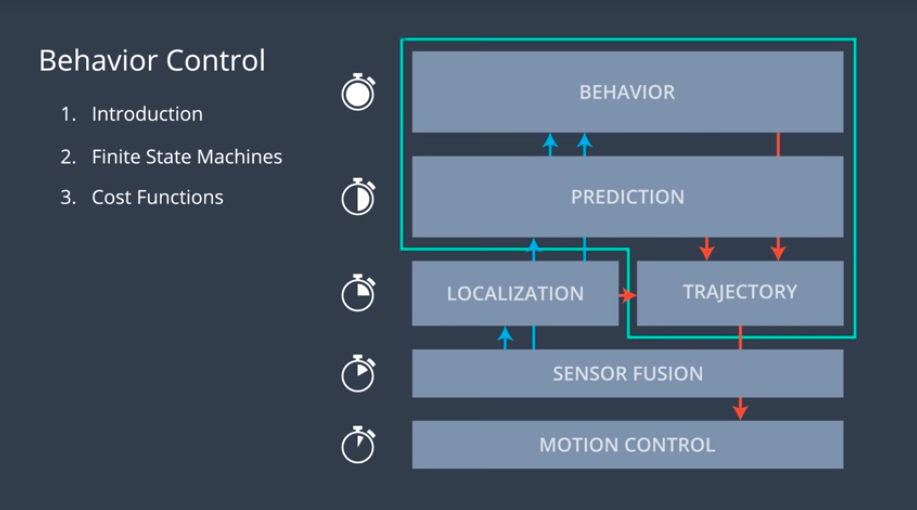
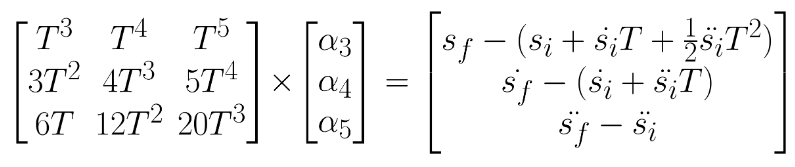Path Planning

Published: 2020-02-09

1. search algorithms used in discrete path planning
2. prediction which is where we use the data from sensor fusion to generate predictions about what all the other objects around us are likely to do.
3. behavior planning: what the car shall do in the next 10 seconds or so.
4. trajectory generation, which is where we create smooth, drivable, and collision-free trajectories.

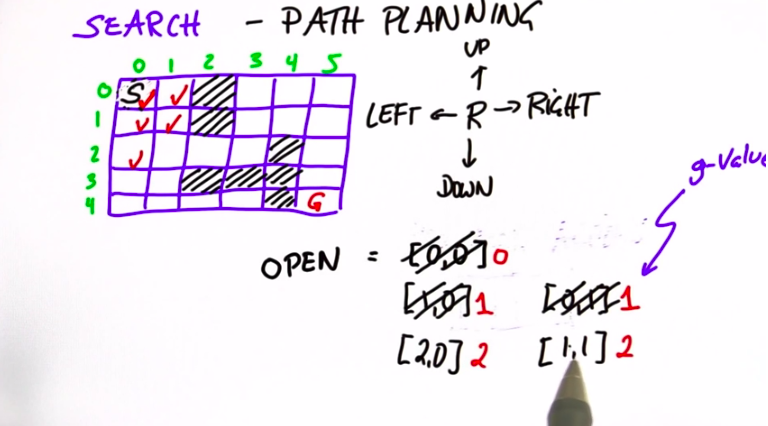
Search #

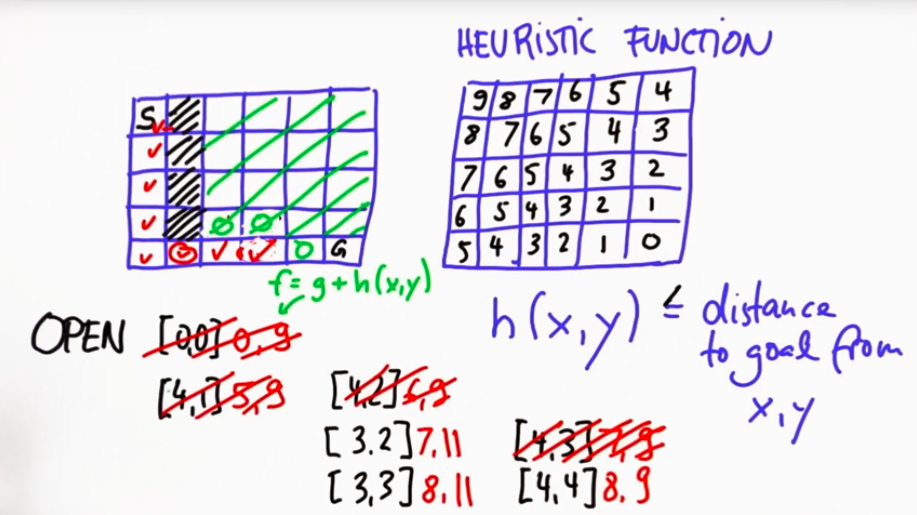
A star with heuristic function:

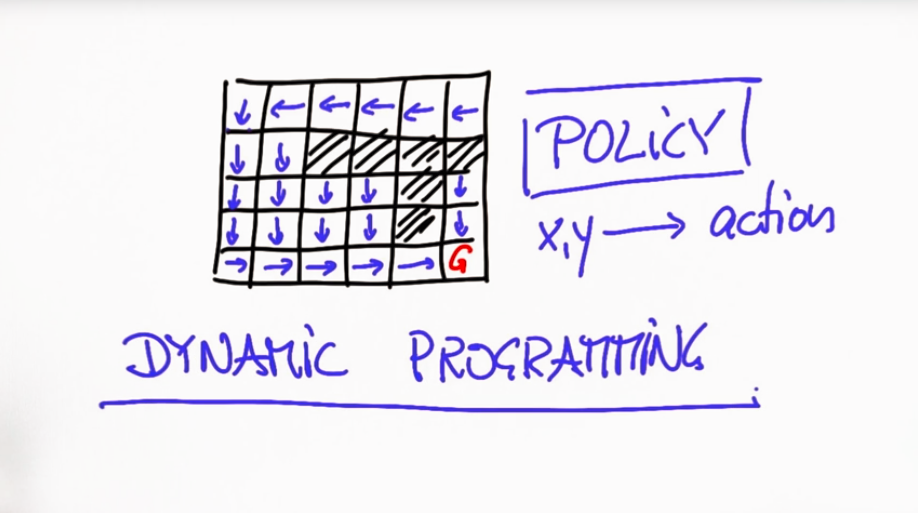
Dynamic Programming:
Given: Map & Goal
Outputs: Best path from ANYWHERE

Prediction #

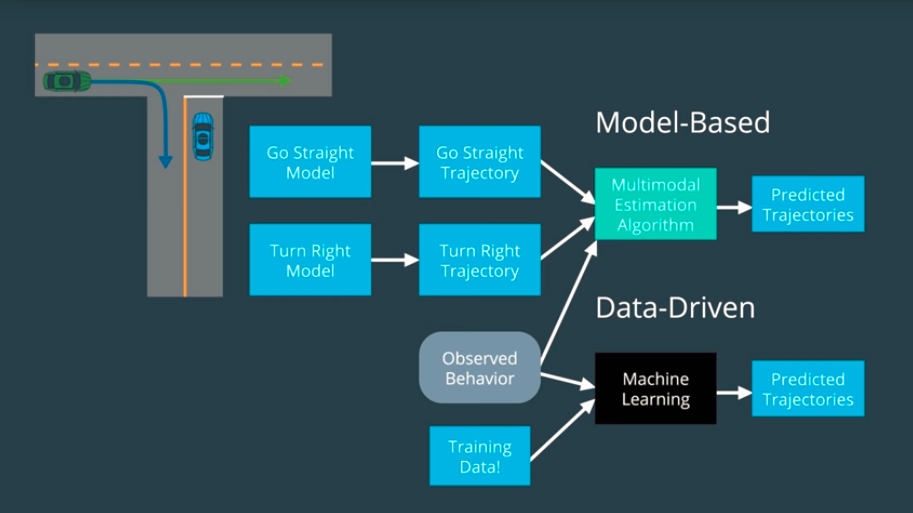
A prediction module uses a map and data from sensor fusion to generate predictions for what all other dynamic objects in view are likely to do. Neither approach (model based or data driven) is strictly better than the other but there are certain situations in which one is more useful than the other.

There are two different approaches to handle the prediction problem: Model-based approach vs Data-driven approach.

Data-driven

Data-driven approaches would be more useful in the following situations:

1. Predicting the behavior of an unidentified object sitting on the road.

Data-driven approaches solve the prediction problem in two phases:

1. Offline training
2. Online Prediction

Offline Training

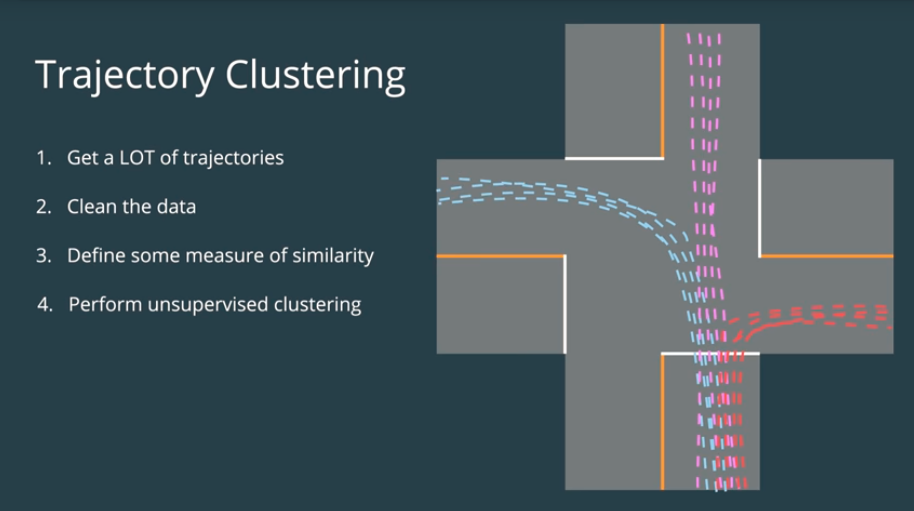
In this phase the goal is to feed some machine learning algorithm a lot of data to train it. For the trajectory clustering example this involved:

1. Define similarity - we first need a definition of similarity that agrees with human common-sense definition.
2. Unsupervised clustering - at this step some machine learning algorithm clusters the trajectories we've observed.
3. Define Prototype Trajectories - for each cluster identify some small number of typical "prototype" trajectories.

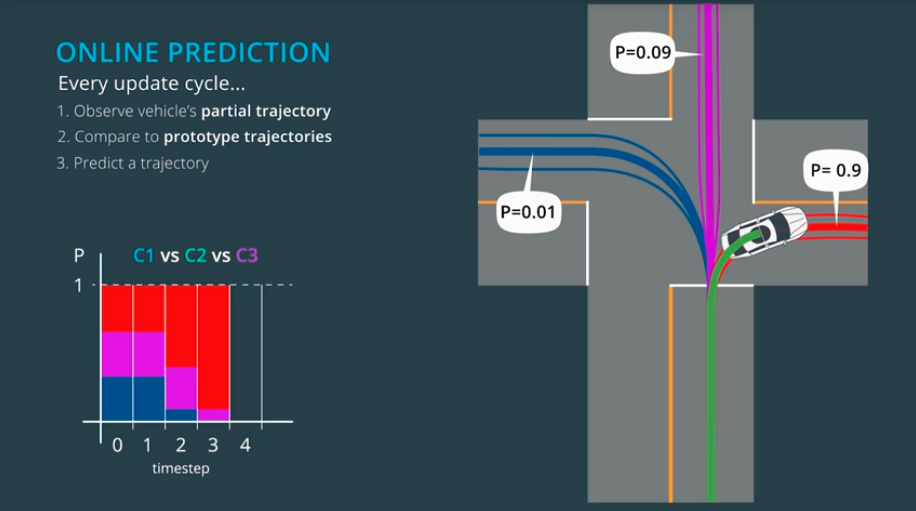
Online Prediction

Once the algorithm is trained we bring it onto the road. When we encounter a situation for which the trained algorithm is appropriate (returning to an intersection for example) we can use that algorithm to actually predict the trajectory of the vehicle. For the intersection example this meant:

1. Observe Partial Trajectory - As the target vehicle drives we can think of it leaving a "partial trajectory" behind it.
2. Compare to Prototype Trajectories - We can compare this partial trajectory to the corresponding parts of the prototype trajectories. When these partial trajectories are more similar (using the same notion of similarity defined earlier) their likelihoods should increase relative to the other trajectories.
3. Generate Predictions - For each cluster we identify the most likely prototype trajectory. We broadcast each of these trajectories along with the associated probability (see the image below).

Model-based

Model-based approaches would be more useful in the following situations:

1. Determining maximum safe turning speed on a wet road.
2. Predicting the behavior of a vehicle on a two lane highway in light traffic.

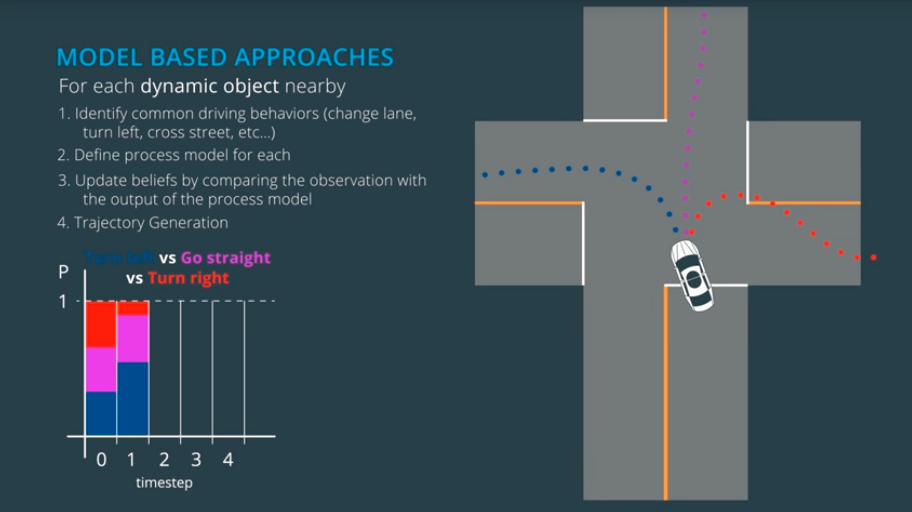
You can think of model based solutions to the prediction problem as also having an "offline" and online component. In that view, this approach requires:

1. Defining process models (offline).
2. Using process models to compare driver behavior to what would be expected for each model.
3. Probabilistically classifying driver intent by comparing the likelihoods of various behaviors with a multiple-model algorithm.
4. Extrapolating process models to generate trajectories.

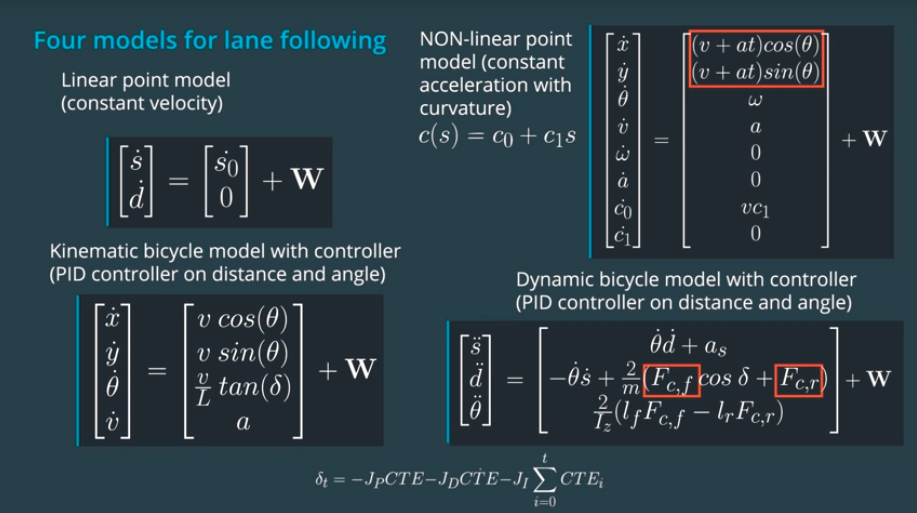
Defining Process Models

You saw how process models can vary in complexity from very simple...

Using Process Models

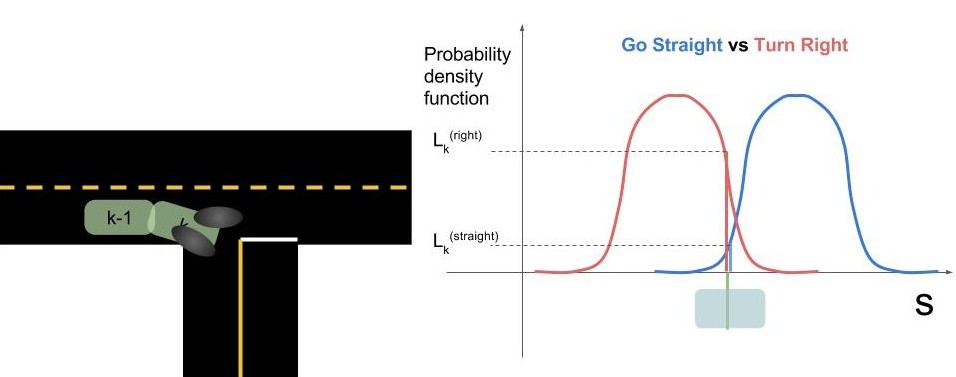
Process Models are first used to compare a target vehicle's observed behavior to the behavior we would expect for each of the maneuvers we've created models for. The pictures below help explain how process models are used to calculate these likelihoods.

On the left we see two images of a car. At time \(k-1\) we predicted where the car would be if it were to go straight vs go right. Then at time \(k\) we look at where the car actually is. The graph on the right shows the car's observed ss coordinate along with the probability distributions for where we expected the car to be at that time. In this case, the ss that we observe is substantially more consistent with turning right than going straight.

Classifying Intent with Multiple Model Algorithm

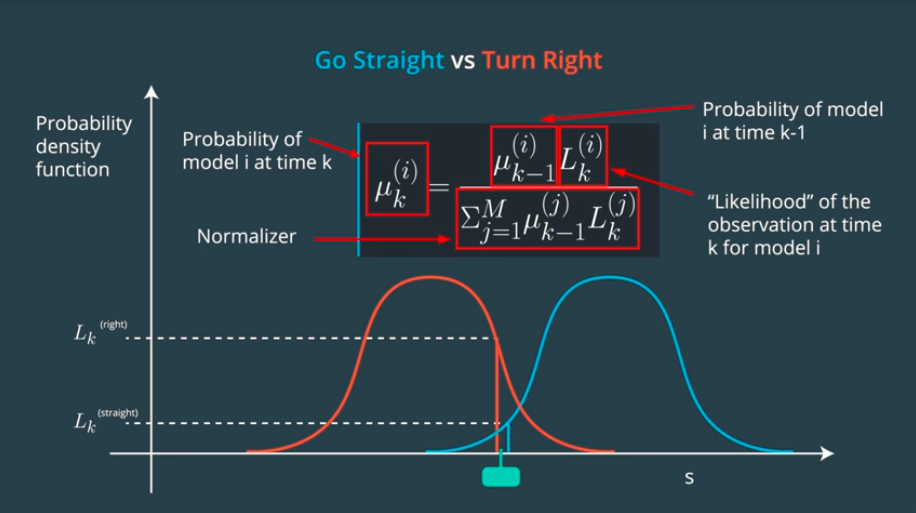
In the image at the top of the page you can see a bar chart representing probabilities of various clusters over time. Multiple model algorithms serve a similar purpose for model based approaches: they are responsible for maintaining beliefs for the probability of each maneuver. The algorithm we discussed is called the Autonomous Multiple Model algorithm (AMM). AMM can be summarized with this equation:

\[ \mu_k^{(i)}=\frac{\mu_{k-1}^{(i)}L_k^{(i)}}{\sum_{j=1}^M\mu_{k-1}^{(j)}L_k^{(j)}} \]

or, if we ignore the denominator (since it just serves to normalize the probabilities), we can capture the essence of this algorithm with

\[ \mu_k^{(i)} \propto \mu_{k-1}^{(i)}L_k^{(i)} \]

where the \(\mu_k^{(i)}\) is the probability that model number \(i\) is the correct model at time \(k\) and \(L_k^{(i)}\) is the likelihood for that model (as computed by comparison to process model).

The paper, "A comparative study of multiple model algorithms for maneuvering target tracking" is a good reference to learn more.

Trajectory Generation

Trajectory generation is straightforward once we have a process model. We simply iterate our model over and over until we've generated a prediction that spans whatever time horizon we are supposed to cover. Note that each iteration of the process model will necessarily add uncertainty to our prediction.

Hybrid Approach

Replace Multimodel Estimator with Machine Learning Method. For more info, please refer to machine learning.

Behavior Planning #

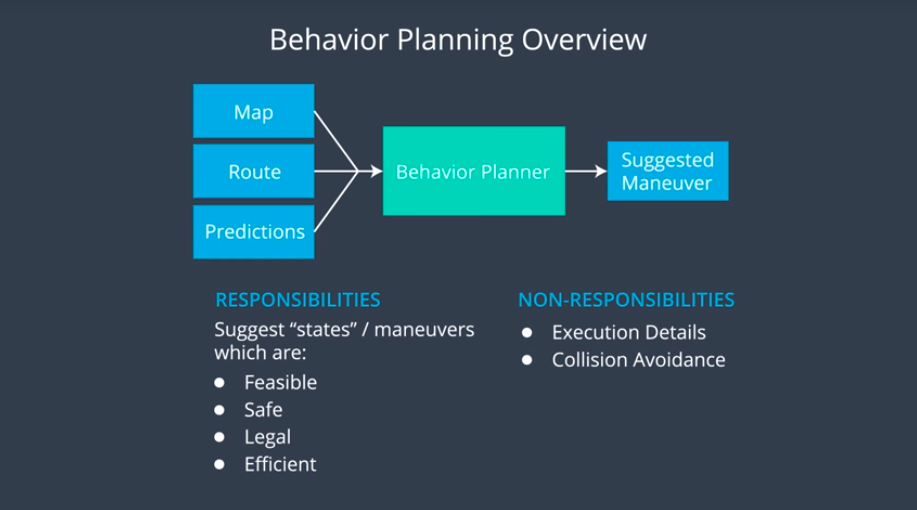
It's possible to suggest a wide variety of behaviors by specifying only a few quantities. For example by specifying only a target lane, a target vehicle (to follow), a target speed, and a time to reach these targets, we can make suggestions as nuanced as "stay in your lane but get behind that vehicle in the right lane so that you can pass it when the gap gets big enough."

The behavior planning team is responsible for providing guidance to the trajectory planner about what sorts of maneuvers they should plan trajectories for.

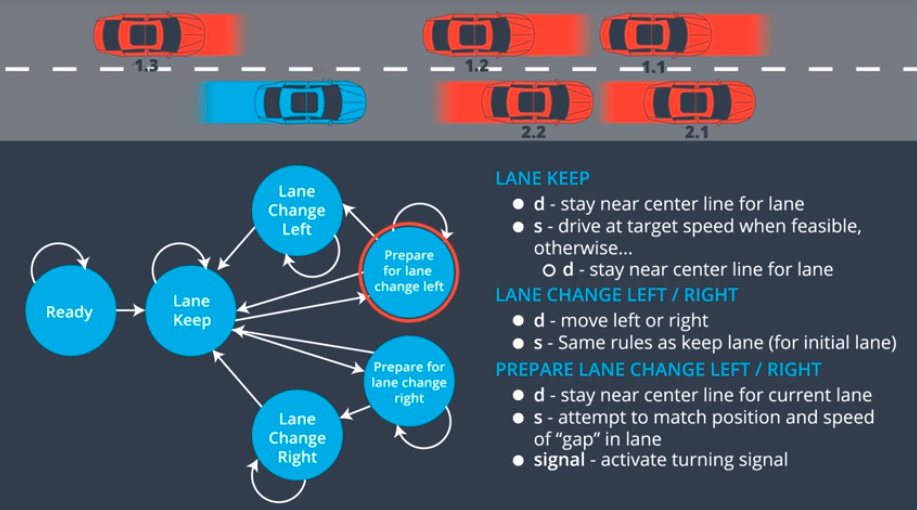
Finite State Machine:

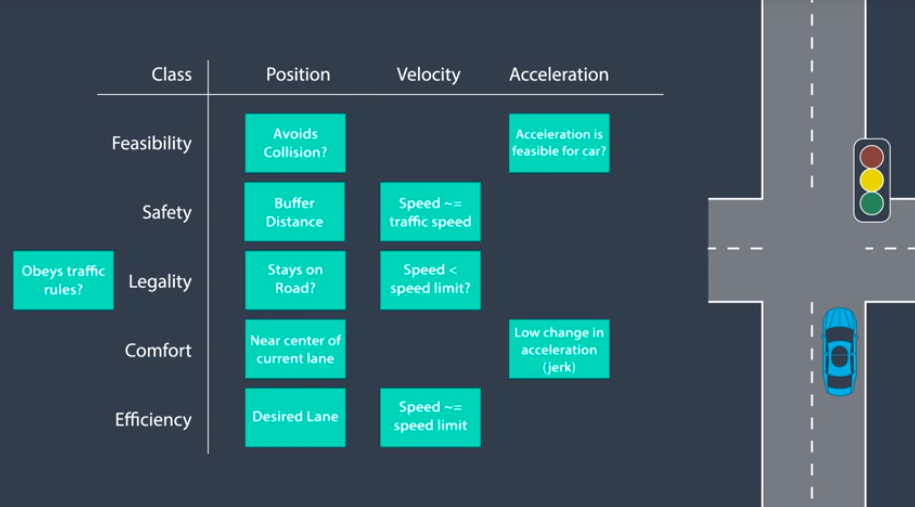
One way to implement a transition function is by generating rough trajectories for each accessible "next state" and then finding the best. To "find the best" we generally use cost functions. We can then figure out how costly each rough trajectory is and then select the state with the lowest cost trajectory.

From what I understood it goes as follows (note that I had to read all the subsequent lessons to get to this understanding): The goal lane is the lane that we should aim to in the long run (e.g. the right most lane for normal driving) and it is used to compute the distance (and cost). Then we need to choose the behaviour according to traffic, here we have different choices when it comes to passing cars and there is the catch that we have two different states to change lane: prepare for change lane and change lane with the former aimed to mach the speed to perform a lane change and the latter to actually move to the adjacent lane. The "final lane" is the lane that the state will be at, while the "intended lane" is the lane that the state is aiming for. So, when we prepare for a lane change the final lane will be the same lane we are at, as we do not change lane at this stage, while the "intended lane" is the lane we are preparing for. When we change lane the "final lane" is the lane we are going to, which corresponds to the "intended lane" as at this stage we are actually changing the lane.

An Programming Examples:
practice
solution

Trajectory Generation #

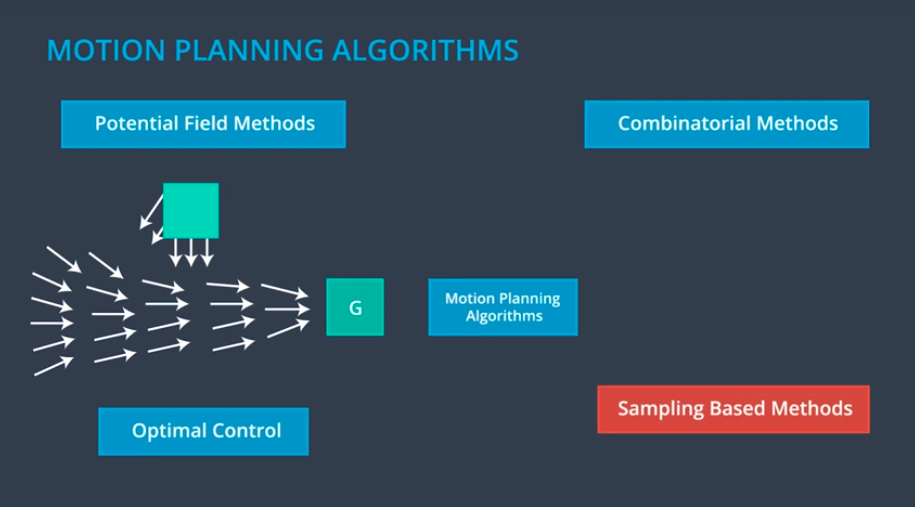
Types of Motion Planning Algorithms

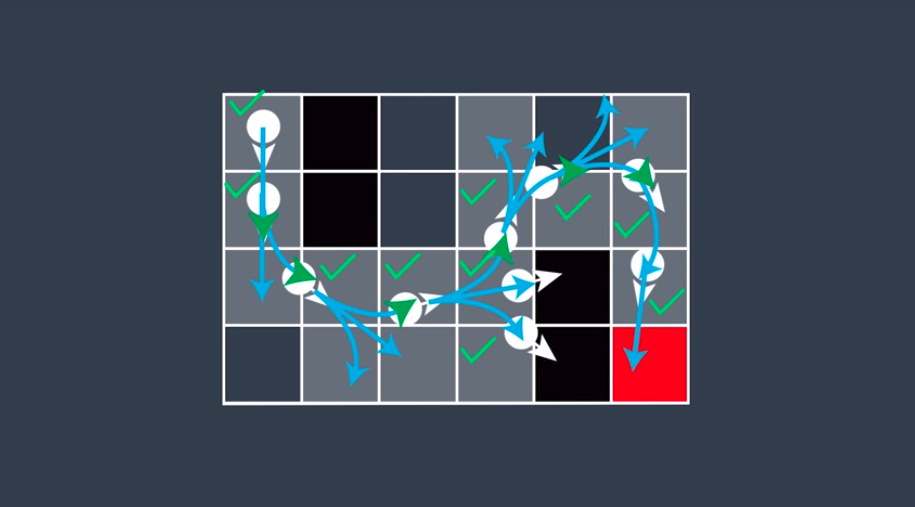
Hybrid A*

1. It uses a continuous search space.
2. It uses an optimistic heuristic function to guide grid cell expansion.
3. Solutions it finds are drivable

Exercise:
hybrid-a-star

Hybrid A* doesn't take advantage of the pre-defined environment information.

Structured Trajectory Generation

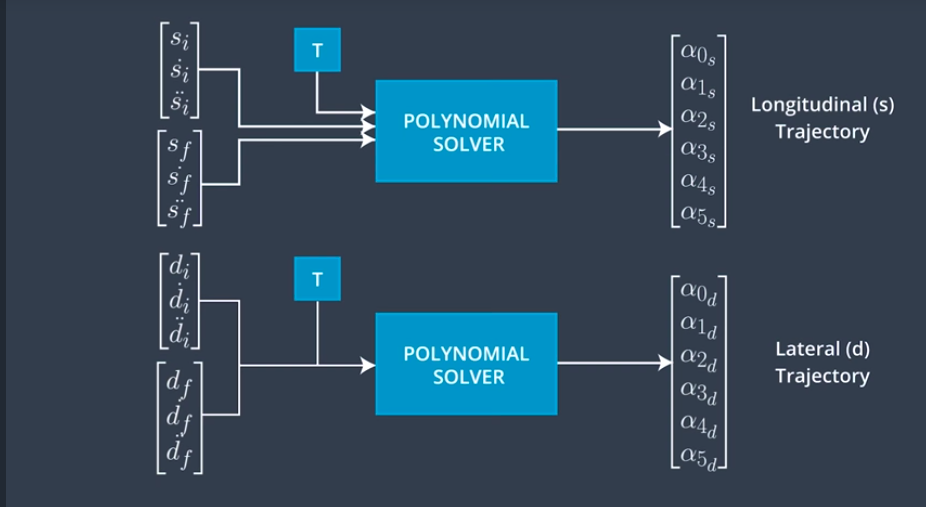
Jerk Minimizing Trajectories

Implementing Feasibility:

When evaluating the feasibility of a potential trajectory, the following quantities should be checked

1. Maximum velocity (with respect to car's capabilities and speed limit)
2. Minimum velocity
3. Maximum acceleration
4. Minimum acceleration
5. Steering angle

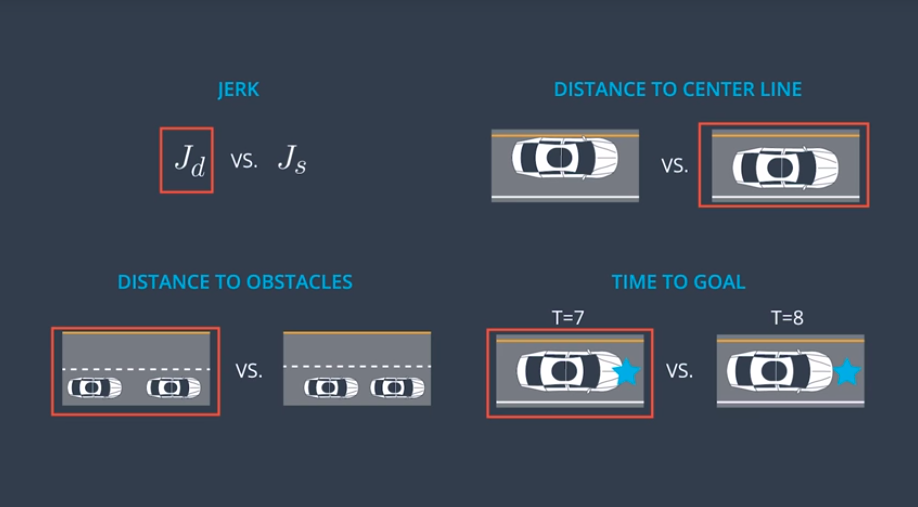
Cost Functions:

If you are interested in learning more about PTG, I've included a link to a paper (below) titled "Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame". It is short and discusses some interesting (and potentially useful) topics like:

1. Cost Functions.
2. Differences between high speed and low speed trajectory generation.
3. Implementation of specific maneuvers relevant to highway driving like following, merging, and velocity keeping.
4. How to combining lateral and longitudinal trajectories.
5. A derivation of the transformation from Frenet coordinates to global coordinates (in the appendix).

Exercises:
Polynomial Playground (making PTG work)
trajectoryexercise2-python3

Paper Reading #

Indoors
Intention-Net: Integrating Planning and Deep Learning for Goal-Directed Autonomous Navigation by S. W. Gao, et. al.

City Navigation
Learning to Navigate in Cities Without a Map by P. Mirowski, et. al.

Intersections
A Look at Motion Planning for Autonomous Vehicles at an Intersection by S. Krishnan, et. al.

Planning in Traffic with Deep Reinforcement Learning
DeepTraffic: Crowdsourced Hyperparameter Tuning of Deep Reinforcement Learning Systems for Multi-Agent Dense Traffic Navigation by L. Fridman, J. Terwilliger and B. Jenik

Next: Bayesian Filter
Previous: Vim