Skip to main content

ORB-SLAM2

Published: 2020-01-04 | Lastmod: 2020-01-29

Table of contents
  1. Tracking
  2. LocalMapping
  3. LoopClosing
  4. Optimization
  5. BowVector & FeatureVector
  6. g2o

Tracking #

Initialization

SearchForInitialization --> Initialize(RANSAC) --> GlobalBundleAdjustemnt --> ComputeSceneMedianDepth

SearchForInitialization:
GetFeaturesInArea --> DescriptorDistance --> ComputeThreeMaxima

ORB特征
Oriented FAST关键点：

  1. 比较像素点周围圆上的像素间亮度的差异
  2. 非极大值抑制，在一定区域内仅保留响应极大值的角点，避免太集中
  3. 对角点计算Harris响应值，仅保留前N个具有最大响应值的角点
  4. 构建金字塔，在金字塔每一层检测角点。实现尺度不变
  5. 灰度质心法，连接图像块的几何中心与质心。实现旋转不变

BRIEF描述子：

  1. 随机选点并比较灰度，组成128维的二进制数组
  2. 使用Hamming distance作为度量，即不同位数的个数

F矩阵
https://zhuanlan.zhihu.com/p/61614421

在求解F和H矩阵之前，应该首先进行特征点归一化，保证坐标均值为0，一阶绝对矩为1。(MVG P67，归一化才能消除坐标变换的影响)
设\(p1\)，\(p2\)为像素坐标，可知：

\[ p_2 = K (RP + t) \\[2mm] p_1 = KP \]

从上述\(p1\)，\(p2\)的关系式出发，导出：

\[ (K^{-1} p_2)^T t^{\wedge} K^{-1} p_2 = 0 = p_2^T K^{-T} t^{\wedge} R K^{-1} p_1 = p_2^T F p_1 \]

一对匹配的像素点可以写1个方程，考虑到尺度等价性，使用八点法即可求解\(F\)矩阵。

TODO: 由基础矩阵F分解出R和t

多余的话
opencv中，cv::findFundamentalMat()如果选择8点法，则是直接将所有点进行最小二乘计算，没有外点剔除功能。
https://stackoverflow.com/questions/25251676/opencv-findfundamentalmat-very-unstable-and-sensitive/48394798

H矩阵
平面方程为：

\[ aX + bY + cZ + d = 0 \\[2mm] -\frac{n^TP}{d} = -1 \]

依旧从\(p1\)，\(p2\)的关系式出发，导出：

\[ p_2 = K (RP + t \cdot (-\frac{n^TP}{d})) = K (R - \frac{tn^T}{d}) K^{-1} p_1 = Hp_1 \]

一对匹配的像素点可以写2个方程，因此4对匹配特征点即可求解\(H\)矩阵。

TODO: 由单应矩阵H恢复出R和t

F与H的评分

\[ S_M = \sum_i\{ \rho_M\left(d_{cr}^2\left(x_c^i,x_r^i,M\right)\right)+ \rho_M\left(d_{rc}^2\left(x_c^i,x_r^i,M\right)\right) \} \\[2mm] \rho_M\left(d^2\right)=\begin{cases} \Gamma - d^2, &\text{if } d^2 < T_M \\ 0, &\text{if } d^2 > T_M\end{cases} \]

其中，\(M\)为\(H\)或者\(F\)。\(T_M\)为距离阈值，根据95%的\(\chi^2\)测试设置。 \(T_H=5.99\)（两个自由度），\(T_F=3.84\)（1个自由度）。这里假设标准差为1个像素。

\(\Gamma\) is defined equal to \(T_H\) so that both models score equally for the same d in their inlier region, again to make the process homogeneous.

\[ R_H=\frac{S_H}{S_H+S_F} \]

select the homography if \(R_H>0.45\), which adequately captures the planar and low parallax cases. Otherwise, we select the fundamental matrix.

三角化
https://blog.csdn.net/weixin_43795395/article/details/93769148
https://www.cnblogs.com/yepeichu/p/10792899.html

已知匹配的像素点，及两帧图像的变换关系，则：

\[ x = PX \\[2mm] x' = P'X \]

根据\(x^\wedge PX = 0\)性质，可得到如下方程：

\[ AX = \begin{bmatrix} xp^{3T}-p^{1T} \\ yp^{3T}-p^{2T} \\ x'p'^{3T}-p'^{1T} \\ y'p'^{3T}-p'^{2T} \end{bmatrix} X = 0 \]

对矩阵\(A\)进行SVD分解，可知：

\[ J(y) = \min \|Ax\| = \min \|UDV^Tx\| = \min \|DV^Tx\| \]

由于对角阵\(D\)是矩阵\(A\)的奇异值从大到小降序排列而成，因此\(J(y)\) 的最小值在\(D\)矩阵奇异值最小的地方取到。可知：

\[ V^Tx = y = [0, 0, 0, 1]^T \\[2mm] x = Vy \]

于是，\(x\)的解就变成了正交矩阵\(V\)的最后一列的列向量。

多余的话——解方程
http://eigen.tuxfamily.org/dox/group__LeastSquares.html

对于方程：

\[ Mx = b \]

可以使用最小二乘解\(x = (M^T M)^{-1} M^T b\)，或者利用QR分解\(x = R^{-1} Q^T b\)。

将b移到左边，并设最后一个参数为1，可转换成如下方程：

\[ Mx = 0 \]

可以通过SVD分解，解对应于\(M\)最小特征值对应的特征向量。关于\(M\)与\(M^T M\)的SVD分解的关系， 可以参考matrix。

Tracking

TrackWithMotionModel
SearchByProjection --> PoseOptimization

SearchByProjection:
GetFeaturesInArea --> DescriptorDistance

TrackWithReferenceKeyFrame
SearchByBow --> PoseOptimization

SearchByBow:
FeatureVector --> DescriptorDistance --> ComputeThreeMaxima

Relocalization
SearchByBow --> EPnP(RANSAC) --> PoseOptimization --> SearchByProjection --> PoseOptimization

EPnP:
https://zhuanlan.zhihu.com/p/59070440

  1. 3D点的齐次坐标被表示为4个控制点齐次坐标的线性组合，然后将其作为已知量拿到相机坐标系下使用。
  2. 结合上一步，将相机坐标系下的空间点坐标，转换成4个控制点在摄像机坐标系下的坐标的线性组合，并结合对应的像素点坐标，建立方程，从而解算出控制点在摄像机坐标系下的坐标。
  3. 最后根据4个控制点，将所有的3D点在摄像机坐标系下的坐标恢复出来。接着采用ICP方法，求解出R和t。

ICP:

  1. 计算两组点的质心位置，然后计算每个点的去质心坐标

\[ q_i = p_i - p \\[2mm] q_i' = p_i' - p' \]

  1. 求取R

\[ W = \sum_{i=1}^n q_i q_i'^T = U \Sigma V^T \\[2mm] R = UV^T \]

  1. 求取t

\[ t = p - R p' \]

image

题外话———未知对应关系的ICP：

  1. 根据距离最小寻找对应点
  2. 根据对应点，计算R和t
  3. 对点云进行转换，计算误差
  4. 重新寻找对应点，不断迭代，直至误差小于某一个值

属于EM算法的一种，待求变量为\( [R | t] \)，隐变量为点的对应关系。先固定第一个变量，优化另一个；再固定另一个，优化第一个变量。通过多次优化后，两个变量都达到最优值。

UpdateLocalMap
SearchByProjection --> PoseOptimization

LocalMapping #

ComputeBow --> SearchForTriangulation --> LocalBA

SearchForTriangulation:
FeatureVector --> DescriptorDistance --> CheckDistEpipolarLine --> ComputeThreeMaxima

关于优化中的卡方分布外点剔除

https://zhuanlan.zhihu.com/p/58556978

高斯白噪声的平方服从卡方分布，有几个观测量就代表几个自由度。

LoopClosing #

TF-IDF

TF: Term Frequency, 指某个特征在单幅图像中出现的频率。

\[ TF_i = \frac{n_i}{n} \]

IDF: Inverse Document Frequency, 指单词在字典中出现的频率越高，则分类图像时区分度越高。

\[ IDF_i = \log \frac{n}{n_i} \]

ComputeSim3

SearchByBow --> sim3(RANSAC) --> SearchBySim3 --> OptimizeSim3 --> SearchByProjection

当两个姿态比较接近时，sim3求解不出有效值。这也是闭环成功后，后续很长一段时间里，不再进行闭环的原因。

sim3:

image

LoopClosing

OptimizeEssentialGraph --> RunGlobalBundleAdjustment

Optimization #

点与位姿优化

\[ \xi^* = \arg \min_\xi \frac{1}{2} \sum_{i=1}^n {\| u_i - \frac{1}{s} K \exp(\xi^\wedge) P_i \|}_2^2 \\[2mm] P' = TP = RP + t \\[2mm] \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix}f_x &0 &c_x \\ 0 &f_y &c_y\end{bmatrix} \begin{bmatrix}\frac{X'}{Z'} \\ \frac{Y'}{Z'}\end{bmatrix} \]

回环（采用左扰动）
实际ORB-SLAM的Pose Graph是采用的Sim3变换。此处仅推导SE(3)上的公式。

\[ \begin{aligned} e_{ij} &= \ln (T_{ij}^{-1} T_i^{-1} T_j)^\vee \\[2mm] &= \ln (T_{ij}^{-1} T_i^{-1} \exp((-\xi_i)^\wedge) T_j)^\vee \\[2mm] &= \ln (T_{ij}^{-1} T_i^{-1} T_j \exp((-Ad(T_j^{-1})\delta\xi_i)^\wedge))^\vee \\[2mm] &= \ln (\exp(e_{ij}^\wedge) \exp((-Ad(T_j^{-1})\delta\xi_i)^\wedge))^\vee \\[2mm] &= \mathcal{J}_r^{-1}(e_{ij}) (-Ad(T_j^{-1})\delta\xi_i) + e_{ij} \\[2mm] \frac{ \partial{e_{ij}} }{ \partial{\delta\xi_i} } &= -\mathcal{J}_r^{-1}(e_{ij}) Ad(T_j^{-1}) \end{aligned} \]

同理可得：

\[ \frac{ \partial{e_{ij}} }{ \partial{\delta\xi_j} } = \mathcal{J}_r^{-1}(e_{ij}) Ad(T_j^{-1}) \]

有以下近似关系：

\[ \mathcal{J}_r^{-1}(e_{ij}) \approx I + \frac{1}{2} \begin{bmatrix} \phi_e^\wedge &\rho_e^\wedge \\ 0 &\phi_e^\wedge \end{bmatrix} \]

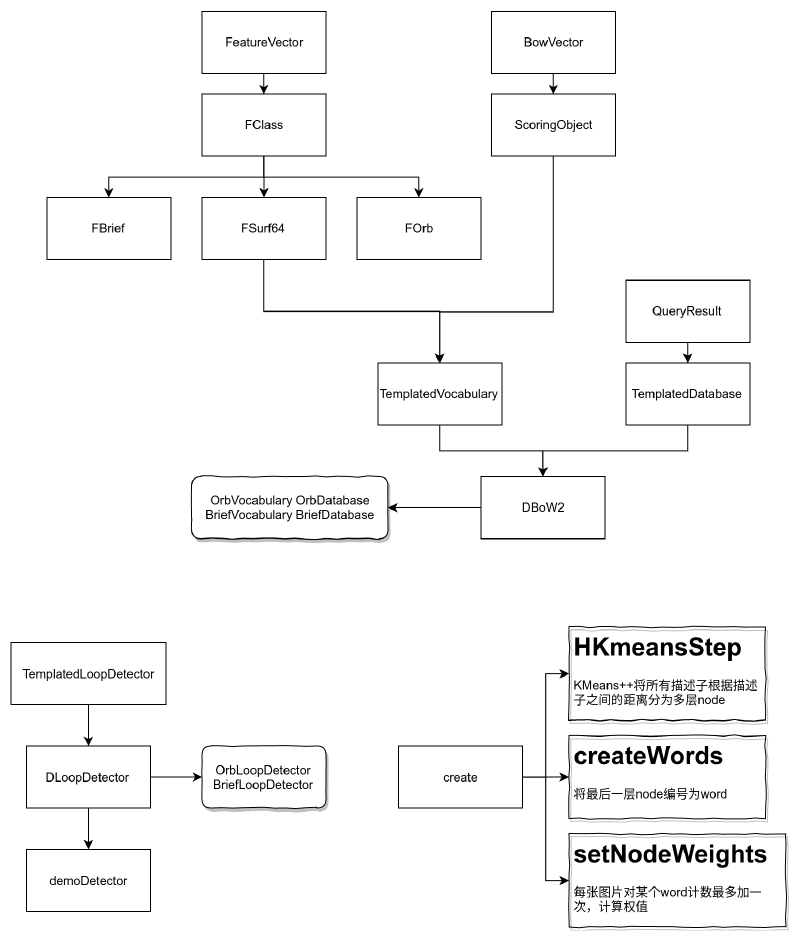
BowVector & FeatureVector #

DBoW2

BowVector存储着叶子节点，信息最细微，仅用在DetectRelocalizationCandidates()函数中，用来选取备选帧。

FeatureVector存储着倒数第4层的节点，信息比较粗糙，用在各种SearchBy*函数中，用来加速特征点的匹配。

FeatureVector --> FClass 计算特征向量之间的距离，用于加速特征点匹配
BowVector --> ScoringObject 计算单词之间的分数，用于匹配回环关键帧

HKmeasStep --> createWords --> setNodeWeights
先使用Kmeans++分为分层node；再将最后一层编码为word；最后每张图片对某个word计数最多加一次，计算权值

g2o #

采用se3表达参数；
首先进行块分解，BlockSolver默认使用舒尔补消除变量;
之后进行线性求解。其中LinearSolverDense直接进行Cholesky分解，LinearSolverEigen需要调用Eigen的稀疏Cholesky分解，且默认不reordering。因为在Schur之后，矩阵比较稠密，reordering影响不大；

Veterx: oplusImpl
Edge: ComputeError & linearizeOplus

https://zhuanlan.zhihu.com/p/100522179


Next: VINS-MONO
Previous: MSCKF