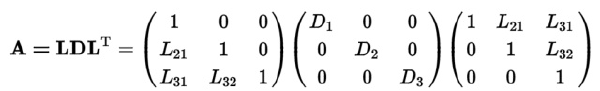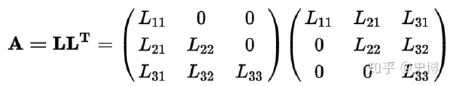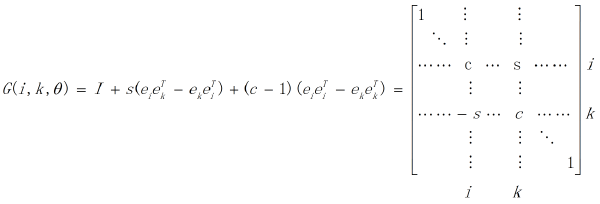Skip to main content

Matrix Decomposition

Published: 2020-01-10 | Lastmod: 2020-11-13

Table of contents
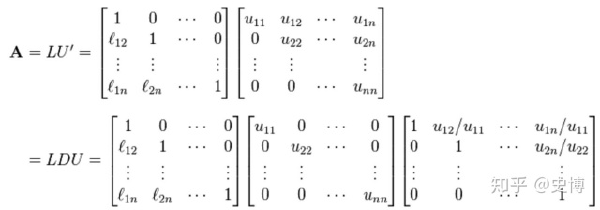
  1. LU & LDU
  2. LDL & LL
  3. QR分解
  4. SVD分解
  5. 作用
  6. 方程求解
  7. NullSpace
  8. 稀疏矩阵的重排序
  9. 建议
  10. SVD & PCA

LU & LDU #

LU & LDU

LDL & LL #

只适用于对称矩阵

LDL

LL

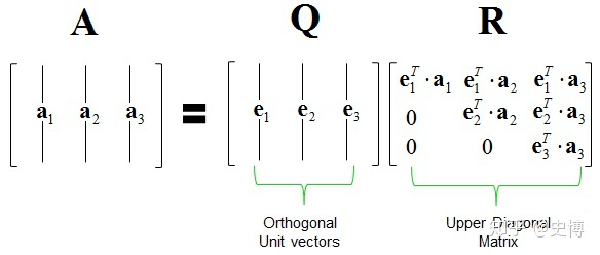
QR分解 #

QR Decomposition

Householder Method

镜像变换，For each i-th column of A, “zero out” rows i+1 and lower

Householder Method

Givens

Don’t reflect; rotate instead, Introduces zeroes into A one at a time

Givens

Gram-Schmidt

Iteratively express each new column vector as a linear combination of previous columns, plus some (normalized) orthogonal component

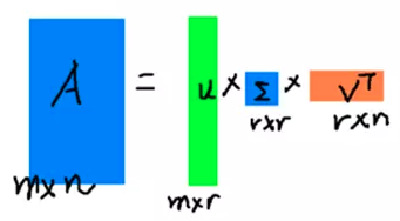
SVD分解 #

SVD

作用 #

对角矩阵：对坐标轴进行缩放
三角矩阵：切变Shear
正交矩阵：旋转

方程求解 #

LU中，LU为三角阵，递归带入求解方程
QR中Q为正交阵，逆矩阵即转置，容易求解
SVD可以用于求解\(Ax=0\)形式的方程，最小特征值对应的特征向量即为解。若方程形式为\(Ax=b\)，将\(b\)移至左侧即可。可参考ORB-SLAM2 Initialization
SLAM中的优化理论（一）—— 线性最小二乘
SLAM中的优化理论（二）- 非线性最小二乘

NullSpace #

Let A be an m-by-n matrix with rank n. QR decomposition finds orthonormal m-by-m matrix Q and upper triangular m-by-n matrix R such that A = QR. If we define Q = [Q1 Q2], where Q1 is m-by-n and Q2 is m-by-(m-n), then the columns of Q2 form the null space of A^T.

QR decomposition is computed either by Gram-Schmidt, Givens rotations, or Householder reflections. They have different stability properties and operation counts.

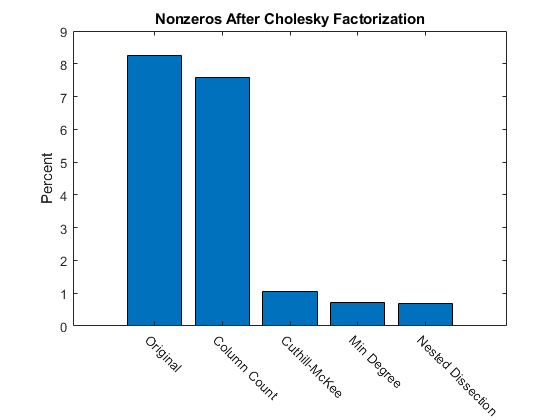
稀疏矩阵的重排序 #

（1）原始稀疏矩阵，进行Cholesky分解后，存在大量非零元素8.24%

Original Sparse Matrix Cholesky Decomposition

（2）采用Nested Dissection Permutation方法进行排序后，再进行Cholesky分解，非零元素显著减少，仅0.68%

Nested Dissection Cholesky Decomposition

（3）各排序方法的比较

SVD

建议 #

  1. 先边缘化掉地图点，因为地图点之间一般是独立的
  2. 再边缘化掉位姿。边缘化位姿时，会造成矩阵稠密
  3. 稠密矩阵解算时，可以先进行排序，再进行Cholesky分解

SVD & PCA #

SVD vs PCA

SVD & PCA

SVD & PCA


Next: Factor Graph
Previous: ROS Navigation Stack