LOAM
Published: 2020-01-14 | Lastmod: 2020-02-02
点云注册 #
坐标系统
IMU与Lidar的坐标系:x轴向前,y轴向左,z轴向上,形成右手坐标系;
LOAM内部坐标系:z轴向前,x轴向左,y轴向上,形成右手坐标系。
关于坐标系统与旋转,请参考Rotation。
重力的处理
imuHandler
需要减去重力在IMU坐标系下的分量,并将坐标系统转换成LOAM内部坐标系。
\[ \begin{aligned} \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix} &=R_{bw} *\begin{pmatrix} 0 \\ 0 \\ g \\ \end{pmatrix} \\[2mm] &=R_x(-roll)*R_y(-pitch)*R_z(-yaw) *\begin{pmatrix} 0 \\ 0 \\ g \\ \end{pmatrix} \\[2mm] &=\begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(roll) & sin(roll) \\ 0 & -sin(roll) & cos(roll) \end{pmatrix} *\begin{pmatrix} cos(pitch) & 0 & -sin(pitch) \\ 0 & 1 & 0 \\ sin(pitch) & 0 & cos(pitch) \end{pmatrix} *\begin{pmatrix} cos(yaw) & sin(yaw) & 0 \\ -sin(yaw) & cos(yaw) & 0 \\ 0 & 0 & 1 \end{pmatrix} *\begin{pmatrix} 0 \\ 0 \\ g \\ \end{pmatrix} \\[2mm] &=\begin{pmatrix} -g\cdot sin(pitch) \\ g\cdot cos(pitch)sin(roll) \\ g\cdot cos(pitch)cos(roll) \end{pmatrix} \end{aligned} \]
对应于下面的代码:
void imuHandler(const sensor_msgs::Imu::ConstPtr& imuIn)
{
float accX = imuIn->linear_acceleration.y - sin(roll) * cos(pitch) * 9.81;
float accY = imuIn->linear_acceleration.z - cos(roll) * cos(pitch) * 9.81;
float accZ = imuIn->linear_acceleration.x + sin(pitch) * 9.81;
}
AccumulateIMUShift
将IMU坐标系下的加速度转换到World坐标系下,并按照匀加速模型,估算两时间间隔内,IMU在Word坐标系下的位置和速度。
\[ \begin{aligned} \begin{pmatrix} a_x' \\ a_y' \\ a_z' \end{pmatrix} &=R_{wb} *\begin{pmatrix} a_x \\ a_y \\ a_z \\ \end{pmatrix} \\[2mm] &=R_y(yaw)*R_x(pitch)*R_z(roll) *\begin{pmatrix} a_x \\ a_y \\ a_z \\ \end{pmatrix} \\[2mm] &=\begin{pmatrix} cos(yaw) & 0 & sin(yaw) \\ 0 & 1 & 0 \\ -sin(yaw) & 0 & cos(yaw) \end{pmatrix} *\begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(pitch) & -sin(pitch) \\ 0 & sin(pitch) & cos(pitch) \end{pmatrix} *\begin{pmatrix} cos(roll) & -sin(roll) & 0 \\ sin(roll) & cos(roll) & 0 \\ 0 & 0 & 1 \end{pmatrix} *\begin{pmatrix} a_x \\ a_y \\ a_z \\ \end{pmatrix} \\[2mm] \end{aligned} \]
void AccumulateIMUShift()
{
float x1 = cos(roll) * accX - sin(roll) * accY;
float y1 = sin(roll) * accX + cos(roll) * accY;
float z1 = accZ;
float x2 = x1;
float y2 = cos(pitch) * y1 - sin(pitch) * z1;
float z2 = sin(pitch) * y1 + cos(pitch) * z1;
accX = cos(yaw) * x2 + sin(yaw) * z2;
accY = y2;
accZ = -sin(yaw) * x2 + cos(yaw) * z2;
}
点云的处理
校准运动畸变
为了保持一次扫描过程中,点的几何关系变化不要太剧烈,我们应该保留匀速运动变化的部分,而将多余的变化量剔除掉。
例如,当扫描仪匀速朝一面墙运动时,形成的点云仍然共面。如果存在加速运动,形成的点云有畸变,将导致不共面。
\[ \begin{aligned} \begin{pmatrix} p_x \\ p_y \\ p_z \end{pmatrix} &=R_{bw} *\begin{pmatrix} \Delta p_x \\ \Delta p_y \\ \Delta p_z \end{pmatrix} \\[2mm] &=R_z(-roll)*R_x(-pitch)*R_y(-yaw) *\begin{pmatrix} \Delta p_x \\ \Delta p_y \\ \Delta p_z \end{pmatrix} \\[2mm] &=\begin{pmatrix} cos(roll) & sin(roll) & 0 \\ -sin(roll) & cos(roll) & 0 \\ 0 & 0 & 1 \end{pmatrix} *\begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(pitch) & sin(pitch) \\ 0 & -sin(pitch) & cos(pitch) \end{pmatrix} *\begin{pmatrix} cos(yaw) & 0 & -sin(yaw) \\ 0 & 1 & 0 \\ sin(yaw) & 0 & cos(yaw) \end{pmatrix} *\begin{pmatrix} \Delta p_x \\ \Delta p_y \\ \Delta p_z \end{pmatrix} \\[2mm] \end{aligned} \]
void ShiftToStartIMU(float pointTime)
{
imuShiftFromStartXCur = imuShiftXCur - imuShiftXStart - imuVeloXStart * pointTime;
imuShiftFromStartYCur = imuShiftYCur - imuShiftYStart - imuVeloYStart * pointTime;
imuShiftFromStartZCur = imuShiftZCur - imuShiftZStart - imuVeloZStart * pointTime;
float x1 = cos(imuYawStart) * imuShiftFromStartXCur - sin(imuYawStart) * imuShiftFromStartZCur;
float y1 = imuShiftFromStartYCur;
float z1 = sin(imuYawStart) * imuShiftFromStartXCur + cos(imuYawStart) * imuShiftFromStartZCur;
float x2 = x1;
float y2 = cos(imuPitchStart) * y1 + sin(imuPitchStart) * z1;
float z2 = -sin(imuPitchStart) * y1 + cos(imuPitchStart) * z1;
imuShiftFromStartXCur = cos(imuRollStart) * x2 + sin(imuRollStart) * y2;
imuShiftFromStartYCur = -sin(imuRollStart) * x2 + cos(imuRollStart) * y2;
imuShiftFromStartZCur = z2;
}
处理每个激光点
- 每个激光点是在当前IMU坐标系下
- 需要先转换到World坐标系下
- 再转到当前帧起始IMU的坐标系下
- 最后去除掉上一步获得的运动畸变
\[ \begin{aligned} \begin{pmatrix} p_x' \\ p_y' \\ p_z' \end{pmatrix} &= R_{b'w} * R_{wb} *\begin{pmatrix} p_x \\ p_y \\ p_z \\ \end{pmatrix} \\[2mm] &=R_z(-roll')*R_x(-pitch')*R_y(-yaw') * R_y(yaw)*R_x(pitch)*R_z(roll) *\begin{pmatrix} p_x \\ p_y \\ p_z \\ \end{pmatrix} \\[2mm] \end{aligned} \]
void TransformToStartIMU(PointType *p)
{
float x1 = cos(imuRollCur) * p->x - sin(imuRollCur) * p->y;
float y1 = sin(imuRollCur) * p->x + cos(imuRollCur) * p->y;
float z1 = p->z;
float x2 = x1;
float y2 = cos(imuPitchCur) * y1 - sin(imuPitchCur) * z1;
float z2 = sin(imuPitchCur) * y1 + cos(imuPitchCur) * z1;
float x3 = cos(imuYawCur) * x2 + sin(imuYawCur) * z2;
float y3 = y2;
float z3 = -sin(imuYawCur) * x2 + cos(imuYawCur) * z2;
float x4 = cos(imuYawStart) * x3 - sin(imuYawStart) * z3;
float y4 = y3;
float z4 = sin(imuYawStart) * x3 + cos(imuYawStart) * z3;
float x5 = x4;
float y5 = cos(imuPitchStart) * y4 + sin(imuPitchStart) * z4;
float z5 = -sin(imuPitchStart) * y4 + cos(imuPitchStart) * z4;
p->x = cos(imuRollStart) * x5 + sin(imuRollStart) * y5 + imuShiftFromStartXCur;
p->y = -sin(imuRollStart) * x5 + cos(imuRollStart) * y5 + imuShiftFromStartYCur;
p->z = z5 + imuShiftFromStartZCur;
}
特征提取
曲率计算
以某点为中心,其前后各5个点,计算10个向量的和。向量的模长表示其在该点处曲率半径。
根据曲率的大小,将点云分为/laser_cloud_sharp, /laser_cloud_less_sharp, /laser_cloud_flat, /laser_cloud_less_flat。
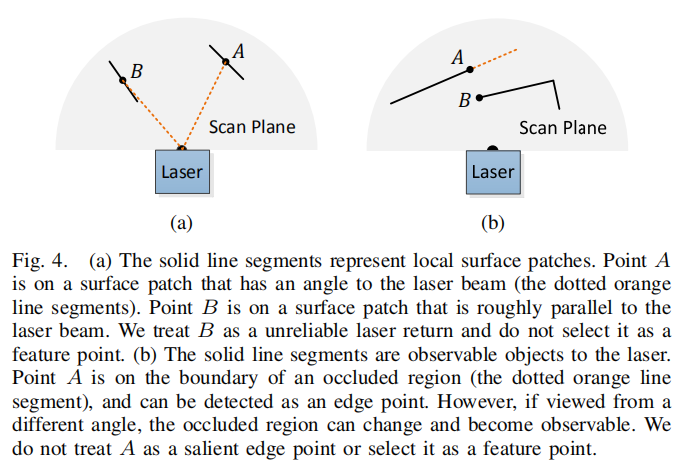
剔除异常点
激光里程计 #
IMU坐标系统转换
转到起始IMU坐标系
点云去除了匀速运动之外的误差,现在就可以合理的假设,上一时刻的点,与当前时刻的点,只有一个匀速运动的点位畸变。 则初始的transform为:
transform[3] -= imuVeloFromStartX * scanPeriod;
transform[4] -= imuVeloFromStartY * scanPeriod;
transform[5] -= imuVeloFromStartZ * scanPeriod;
这里定义的transform比较特殊,在理解时需要特别注意。与下文2.3节的优化相对应。
将每个激光点坐标,按照匀速运动假设,将旋转、平移的畸变量去掉,转换到IMU起始坐标系下。
\[ \begin{aligned} \begin{pmatrix} p_x' \\ p_y' \\ p_z' \end{pmatrix} &= R_{b'b} *\begin{pmatrix} p_x - t_x \\ p_y - t_y \\ p_z - t_z \end{pmatrix} \\[2mm] &=R_y(-yaw)*R_x(-pitch)*R_z(-roll) *\begin{pmatrix} p_x - t_x \\ p_y - t_y \\ p_z - t_z \end{pmatrix} \\[2mm] \end{aligned} \]
void TransformToStart(PointType const * const pi, PointType * const po)
{
float s = 10 * (pi->intensity - int(pi->intensity));
float rx = s * transform[0];
float ry = s * transform[1];
float rz = s * transform[2];
float tx = s * transform[3];
float ty = s * transform[4];
float tz = s * transform[5];
float x1 = cos(rz) * (pi->x - tx) + sin(rz) * (pi->y - ty);
float y1 = -sin(rz) * (pi->x - tx) + cos(rz) * (pi->y - ty);
float z1 = (pi->z - tz);
float x2 = x1;
float y2 = cos(rx) * y1 + sin(rx) * z1;
float z2 = -sin(rx) * y1 + cos(rx) * z1;
po->x = cos(ry) * x2 - sin(ry) * z2;
po->y = y2;
po->z = sin(ry) * x2 + cos(ry) * z2;
po->intensity = pi->intensity;
}转到结束IMU坐标系
在处理结束后,要将这一帧的点坐标转到IMU结束时刻下,以便下一次的帧间匹配。需要进行如下步骤:
- 转到该帧IMU起始坐标系
- 转到该帧IMU结束坐标系
- 加上最后一个点对应的匀速运动之外的畸变,并转到起始World坐标系下
- 最后转到结束IMU坐标系下。
\[ TODO \]
void TransformToEnd(PointType const * const pi, PointType * const po)
{
float s = 10 * (pi->intensity - int(pi->intensity));
//rotation 1
float rx = s * transform[0];
float ry = s * transform[1];
float rz = s * transform[2];
float tx = s * transform[3];
float ty = s * transform[4];
float tz = s * transform[5];
float x1 = cos(rz) * (pi->x - tx) + sin(rz) * (pi->y - ty);
float y1 = -sin(rz) * (pi->x - tx) + cos(rz) * (pi->y - ty);
float z1 = (pi->z - tz);
float x2 = x1;
float y2 = cos(rx) * y1 + sin(rx) * z1;
float z2 = -sin(rx) * y1 + cos(rx) * z1;
float x3 = cos(ry) * x2 - sin(ry) * z2;
float y3 = y2;
float z3 = sin(ry) * x2 + cos(ry) * z2;
//rotation 2
rx = transform[0];
ry = transform[1];
rz = transform[2];
tx = transform[3];
ty = transform[4];
tz = transform[5];
float x4 = cos(ry) * x3 + sin(ry) * z3;
float y4 = y3;
float z4 = -sin(ry) * x3 + cos(ry) * z3;
float x5 = x4;
float y5 = cos(rx) * y4 - sin(rx) * z4;
float z5 = sin(rx) * y4 + cos(rx) * z4;
float x6 = cos(rz) * x5 - sin(rz) * y5 + tx;
float y6 = sin(rz) * x5 + cos(rz) * y5 + ty;
float z6 = z5 + tz;
//rotation 3
float x7 = cos(imuRollStart) * (x6 - imuShiftFromStartX)
- sin(imuRollStart) * (y6 - imuShiftFromStartY);
float y7 = sin(imuRollStart) * (x6 - imuShiftFromStartX)
+ cos(imuRollStart) * (y6 - imuShiftFromStartY);
float z7 = z6 - imuShiftFromStartZ;
float x8 = x7;
float y8 = cos(imuPitchStart) * y7 - sin(imuPitchStart) * z7;
float z8 = sin(imuPitchStart) * y7 + cos(imuPitchStart) * z7;
float x9 = cos(imuYawStart) * x8 + sin(imuYawStart) * z8;
float y9 = y8;
float z9 = -sin(imuYawStart) * x8 + cos(imuYawStart) * z8;
//rotation 4
float x10 = cos(imuYawLast) * x9 - sin(imuYawLast) * z9;
float y10 = y9;
float z10 = sin(imuYawLast) * x9 + cos(imuYawLast) * z9;
float x11 = x10;
float y11 = cos(imuPitchLast) * y10 + sin(imuPitchLast) * z10;
float z11 = -sin(imuPitchLast) * y10 + cos(imuPitchLast) * z10;
po->x = cos(imuRollLast) * x11 + sin(imuRollLast) * y11;
po->y = -sin(imuRollLast) * x11 + cos(imuRollLast) * y11;
po->z = z11;
po->intensity = int(pi->intensity);
}
IMU累计
AccumulateRotation
代码直接实现了将两个旋转量累加起来,得到累加后的欧拉角。代码实现效率高,但是不易读。 将旋转矩阵展开以后可以看到其相应关系。
Rwb1 = Ry(y1) * Rx(x1) * Rz(z1);
Rbw2 = Ry(y2) * Rx(x2) * Rz(z2);
Rwb3 = Rwb1 * Rbw2
=
[ cos(y)*cos(z) + sin(x)*sin(y)*sin(z), cos(z)*sin(x)*sin(y) - cos(y)*sin(z), cos(x)*sin(y)]
[ cos(x)*sin(z), cos(x)*cos(z), -sin(x)]
[ cos(y)*sin(x)*sin(z) - cos(z)*sin(y), sin(y)*sin(z) + cos(y)*cos(z)*sin(x), cos(x)*cos(y)]
=
[ (cos(y1)*cos(z1) + sin(x1)*sin(y1)*sin(z1))*(cos(y2)*cos(z2) + sin(x2)*sin(y2)*sin(z2)) - cos(x1)*sin(y1)*(cos(z2)*sin(y2) - cos(y2)*sin(x2)*sin(z2)) - cos(x2)*sin(z2)*(cos(y1)*sin(z1) - cos(z1)*sin(x1)*sin(y1)), cos(x1)*sin(y1)*(sin(y2)*sin(z2) + cos(y2)*cos(z2)*sin(x2)) - cos(x2)*cos(z2)*(cos(y1)*sin(z1) - cos(z1)*sin(x1)*sin(y1)) - (cos(y1)*cos(z1) + sin(x1)*sin(y1)*sin(z1))*(cos(y2)*sin(z2) - cos(z2)*sin(x2)*sin(y2)), sin(x2)*(cos(y1)*sin(z1) - cos(z1)*sin(x1)*sin(y1)) + cos(x2)*sin(y2)*(cos(y1)*cos(z1) + sin(x1)*sin(y1)*sin(z1)) + cos(x1)*cos(x2)*cos(y2)*sin(y1)]
[ sin(x1)*(cos(z2)*sin(y2) - cos(y2)*sin(x2)*sin(z2)) + cos(x1)*sin(z1)*(cos(y2)*cos(z2) + sin(x2)*sin(y2)*sin(z2)) + cos(x1)*cos(x2)*cos(z1)*sin(z2), cos(x1)*cos(x2)*cos(z1)*cos(z2) - cos(x1)*sin(z1)*(cos(y2)*sin(z2) - cos(z2)*sin(x2)*sin(y2)) - sin(x1)*(sin(y2)*sin(z2) + cos(y2)*cos(z2)*sin(x2)), cos(x1)*cos(x2)*sin(y2)*sin(z1) - cos(x1)*cos(z1)*sin(x2) - cos(x2)*cos(y2)*sin(x1)]
[ cos(x2)*sin(z2)*(sin(y1)*sin(z1) + cos(y1)*cos(z1)*sin(x1)) - cos(x1)*cos(y1)*(cos(z2)*sin(y2) - cos(y2)*sin(x2)*sin(z2)) - (cos(z1)*sin(y1) - cos(y1)*sin(x1)*sin(z1))*(cos(y2)*cos(z2) + sin(x2)*sin(y2)*sin(z2)), (cos(z1)*sin(y1) - cos(y1)*sin(x1)*sin(z1))*(cos(y2)*sin(z2) - cos(z2)*sin(x2)*sin(y2)) + cos(x1)*cos(y1)*(sin(y2)*sin(z2) + cos(y2)*cos(z2)*sin(x2)) + cos(x2)*cos(z2)*(sin(y1)*sin(z1) + cos(y1)*cos(z1)*sin(x1)), cos(x1)*cos(x2)*cos(y1)*cos(y2) - cos(x2)*sin(y2)*(cos(z1)*sin(y1) - cos(y1)*sin(x1)*sin(z1)) - sin(x2)*(sin(y1)*sin(z1) + cos(y1)*cos(z1)*sin(x1))]可以看到,代码与上面的公式是一一对应的。
void AccumulateRotation(float cx, float cy, float cz, float lx, float ly, float lz,
float &ox, float &oy, float &oz)
{
float srx = cos(lx)*cos(cx)*sin(ly)*sin(cz) - cos(cx)*cos(cz)*sin(lx) - cos(lx)*cos(ly)*sin(cx);
ox = -asin(srx);
float srycrx = sin(lx)*(cos(cy)*sin(cz) - cos(cz)*sin(cx)*sin(cy)) + cos(lx)*sin(ly)*(cos(cy)*cos(cz)
+ sin(cx)*sin(cy)*sin(cz)) + cos(lx)*cos(ly)*cos(cx)*sin(cy);
float crycrx = cos(lx)*cos(ly)*cos(cx)*cos(cy) - cos(lx)*sin(ly)*(cos(cz)*sin(cy)
- cos(cy)*sin(cx)*sin(cz)) - sin(lx)*(sin(cy)*sin(cz) + cos(cy)*cos(cz)*sin(cx));
oy = atan2(srycrx / cos(ox), crycrx / cos(ox));
float srzcrx = sin(cx)*(cos(lz)*sin(ly) - cos(ly)*sin(lx)*sin(lz)) + cos(cx)*sin(cz)*(cos(ly)*cos(lz)
+ sin(lx)*sin(ly)*sin(lz)) + cos(lx)*cos(cx)*cos(cz)*sin(lz);
float crzcrx = cos(lx)*cos(lz)*cos(cx)*cos(cz) - cos(cx)*sin(cz)*(cos(ly)*sin(lz)
- cos(lz)*sin(lx)*sin(ly)) - sin(cx)*(sin(ly)*sin(lz) + cos(ly)*cos(lz)*sin(lx));
oz = atan2(srzcrx / cos(ox), crzcrx / cos(ox));
}
PluginIMURotation
\[ R_x = R_{Last} * R_{Start}^{-1} * R_x \]
R1 = Ry(alz) * Rx(alx) * Rz(aly);
R2 = Rz(-bly) * Rx(-blx) * Ry(-blz);
R3 = Ry(bcz) * Rx(bcx) * Rz(bcy);
R = R1 * R2 * R3
=
[ cos(y)*cos(z) + sin(x)*sin(y)*sin(z), cos(z)*sin(x)*sin(y) - cos(y)*sin(z), cos(x)*sin(y)]
[ cos(x)*sin(z), cos(x)*cos(z), -sin(x)]
[ cos(y)*sin(x)*sin(z) - cos(z)*sin(y), sin(y)*sin(z) + cos(y)*cos(z)*sin(x), cos(x)*cos(y)]
=
[ (cos(bcy)*sin(bcz) - cos(bcz)*sin(bcx)*sin(bcy))*((cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz))*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) + (cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz))*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) - cos(alx)*cos(blx)*cos(blz)*sin(alz)) + (cos(bcy)*cos(bcz) + sin(bcx)*sin(bcy)*sin(bcz))*((cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz))*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) + (cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz))*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) + cos(alx)*cos(blx)*sin(alz)*sin(blz)) - cos(bcx)*sin(bcy)*(cos(blx)*cos(bly)*(cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz)) - cos(blx)*sin(bly)*(cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz)) + cos(alx)*sin(alz)*sin(blx)), - (sin(bcy)*sin(bcz) + cos(bcy)*cos(bcz)*sin(bcx))*((cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz))*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) + (cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz))*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) - cos(alx)*cos(blx)*cos(blz)*sin(alz)) - (cos(bcz)*sin(bcy) - cos(bcy)*sin(bcx)*sin(bcz))*((cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz))*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) + (cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz))*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) + cos(alx)*cos(blx)*sin(alz)*sin(blz)) - cos(bcx)*cos(bcy)*(cos(blx)*cos(bly)*(cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz)) - cos(blx)*sin(bly)*(cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz)) + cos(alx)*sin(alz)*sin(blx)), sin(bcx)*(cos(blx)*cos(bly)*(cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz)) - cos(blx)*sin(bly)*(cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz)) + cos(alx)*sin(alz)*sin(blx)) - cos(bcx)*cos(bcz)*((cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz))*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) + (cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz))*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) - cos(alx)*cos(blx)*cos(blz)*sin(alz)) + cos(bcx)*sin(bcz)*((cos(aly)*cos(alz) + sin(alx)*sin(aly)*sin(alz))*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) + (cos(alz)*sin(aly) - cos(aly)*sin(alx)*sin(alz))*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) + cos(alx)*cos(blx)*sin(alz)*sin(blz))]
[ (cos(bcy)*sin(bcz) - cos(bcz)*sin(bcx)*sin(bcy))*(cos(alx)*sin(aly)*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) - cos(alx)*cos(aly)*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) + cos(blx)*cos(blz)*sin(alx)) - (cos(bcy)*cos(bcz) + sin(bcx)*sin(bcy)*sin(bcz))*(cos(alx)*cos(aly)*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) - cos(alx)*sin(aly)*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) + cos(blx)*sin(alx)*sin(blz)) + cos(bcx)*sin(bcy)*(sin(alx)*sin(blx) + cos(alx)*cos(aly)*cos(blx)*cos(bly) + cos(alx)*cos(blx)*sin(aly)*sin(bly)), (cos(bcz)*sin(bcy) - cos(bcy)*sin(bcx)*sin(bcz))*(cos(alx)*cos(aly)*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) - cos(alx)*sin(aly)*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) + cos(blx)*sin(alx)*sin(blz)) - (sin(bcy)*sin(bcz) + cos(bcy)*cos(bcz)*sin(bcx))*(cos(alx)*sin(aly)*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) - cos(alx)*cos(aly)*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) + cos(blx)*cos(blz)*sin(alx)) + cos(bcx)*cos(bcy)*(sin(alx)*sin(blx) + cos(alx)*cos(aly)*cos(blx)*cos(bly) + cos(alx)*cos(blx)*sin(aly)*sin(bly)), - sin(bcx)*(sin(alx)*sin(blx) + cos(alx)*cos(aly)*cos(blx)*cos(bly) + cos(alx)*cos(blx)*sin(aly)*sin(bly)) - cos(bcx)*cos(bcz)*(cos(alx)*sin(aly)*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) - cos(alx)*cos(aly)*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) + cos(blx)*cos(blz)*sin(alx)) - cos(bcx)*sin(bcz)*(cos(alx)*cos(aly)*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) - cos(alx)*sin(aly)*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) + cos(blx)*sin(alx)*sin(blz))]
[ - (cos(bcy)*sin(bcz) - cos(bcz)*sin(bcx)*sin(bcy))*((sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx))*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) + (cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly))*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) + cos(alx)*cos(alz)*cos(blx)*cos(blz)) - (cos(bcy)*cos(bcz) + sin(bcx)*sin(bcy)*sin(bcz))*((sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx))*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) + (cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly))*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) - cos(alx)*cos(alz)*cos(blx)*sin(blz)) - cos(bcx)*sin(bcy)*(cos(blx)*sin(bly)*(cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly)) - cos(blx)*cos(bly)*(sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx)) + cos(alx)*cos(alz)*sin(blx)), (sin(bcy)*sin(bcz) + cos(bcy)*cos(bcz)*sin(bcx))*((sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx))*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) + (cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly))*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) + cos(alx)*cos(alz)*cos(blx)*cos(blz)) + (cos(bcz)*sin(bcy) - cos(bcy)*sin(bcx)*sin(bcz))*((sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx))*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) + (cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly))*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) - cos(alx)*cos(alz)*cos(blx)*sin(blz)) - cos(bcx)*cos(bcy)*(cos(blx)*sin(bly)*(cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly)) - cos(blx)*cos(bly)*(sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx)) + cos(alx)*cos(alz)*sin(blx)), sin(bcx)*(cos(blx)*sin(bly)*(cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly)) - cos(blx)*cos(bly)*(sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx)) + cos(alx)*cos(alz)*sin(blx)) + cos(bcx)*cos(bcz)*((sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx))*(sin(bly)*sin(blz) + cos(bly)*cos(blz)*sin(blx)) + (cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly))*(cos(bly)*sin(blz) - cos(blz)*sin(blx)*sin(bly)) + cos(alx)*cos(alz)*cos(blx)*cos(blz)) - cos(bcx)*sin(bcz)*((sin(aly)*sin(alz) + cos(aly)*cos(alz)*sin(alx))*(cos(blz)*sin(bly) - cos(bly)*sin(blx)*sin(blz)) + (cos(aly)*sin(alz) - cos(alz)*sin(alx)*sin(aly))*(cos(bly)*cos(blz) + sin(blx)*sin(bly)*sin(blz)) - cos(alx)*cos(alz)*cos(blx)*sin(blz))](这个函数的作用后面还要研究下。\(z\)轴和\(y\)轴要互换以后,才跟代码对的上)
虽然直接求解效率高,但是可读性实在太差。通过矩阵的展开、对比、分析,发现与代码一一对应。 例如srx与\(R(2,3)\)是相对应的。
void PluginIMURotation(float bcx, float bcy, float bcz, float blx, float bly, float blz,
float alx, float aly, float alz, float &acx, float &acy, float &acz)
{
float srx = -sbcx*(salx*sblx + calx*caly*cblx*cbly + calx*cblx*saly*sbly)
- cbcx*cbcz*(calx*saly*(cbly*sblz - cblz*sblx*sbly)
- calx*caly*(sbly*sblz + cbly*cblz*sblx) + cblx*cblz*salx)
- cbcx*sbcz*(calx*caly*(cblz*sbly - cbly*sblx*sblz)
- calx*saly*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sblz);
acx = -asin(srx);
float srycrx = (cbcy*sbcz - cbcz*sbcx*sbcy)*(calx*saly*(cbly*sblz - cblz*sblx*sbly)
- calx*caly*(sbly*sblz + cbly*cblz*sblx) + cblx*cblz*salx)
- (cbcy*cbcz + sbcx*sbcy*sbcz)*(calx*caly*(cblz*sbly - cbly*sblx*sblz)
- calx*saly*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sblz)
+ cbcx*sbcy*(salx*sblx + calx*caly*cblx*cbly + calx*cblx*saly*sbly);
float crycrx = (cbcz*sbcy - cbcy*sbcx*sbcz)*(calx*caly*(cblz*sbly - cbly*sblx*sblz)
- calx*saly*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sblz)
- (sbcy*sbcz + cbcy*cbcz*sbcx)*(calx*saly*(cbly*sblz - cblz*sblx*sbly)
- calx*caly*(sbly*sblz + cbly*cblz*sblx) + cblx*cblz*salx)
+ cbcx*cbcy*(salx*sblx + calx*caly*cblx*cbly + calx*cblx*saly*sbly);
acy = atan2(srycrx / cos(acx), crycrx / cos(acx));
float srzcrx = sbcx*(cblx*cbly*(calz*saly - caly*salx*salz)
- cblx*sbly*(caly*calz + salx*saly*salz) + calx*salz*sblx)
- cbcx*cbcz*((caly*calz + salx*saly*salz)*(cbly*sblz - cblz*sblx*sbly)
+ (calz*saly - caly*salx*salz)*(sbly*sblz + cbly*cblz*sblx)
- calx*cblx*cblz*salz) + cbcx*sbcz*((caly*calz + salx*saly*salz)*(cbly*cblz
+ sblx*sbly*sblz) + (calz*saly - caly*salx*salz)*(cblz*sbly - cbly*sblx*sblz)
+ calx*cblx*salz*sblz);
float crzcrx = sbcx*(cblx*sbly*(caly*salz - calz*salx*saly)
- cblx*cbly*(saly*salz + caly*calz*salx) + calx*calz*sblx)
+ cbcx*cbcz*((saly*salz + caly*calz*salx)*(sbly*sblz + cbly*cblz*sblx)
+ (caly*salz - calz*salx*saly)*(cbly*sblz - cblz*sblx*sbly)
+ calx*calz*cblx*cblz) - cbcx*sbcz*((saly*salz + caly*calz*salx)*(cblz*sbly
- cbly*sblx*sblz) + (caly*salz - calz*salx*saly)*(cbly*cblz + sblx*sbly*sblz)
- calx*calz*cblx*sblz);
acz = atan2(srzcrx / cos(acx), crzcrx / cos(acx));
}
观测方程
\[ d=D(p_1) \\[2mm] p_1 = s R (p_2 - s t) \]
其中\(D(\cdot)\)对应于下面介绍的点线方程和点面方程;\(R\)旋转矩阵中包括待估的3个欧拉角\(\alpha,\beta,\gamma\),\(t\)包括3个平移量\(x,y,z\)。 残差\(d\)与待估参数\(X\)的关系:
\[ \frac{\partial d}{\partial X} = \frac{\partial d}{\partial p_1} \cdot \frac{\partial p_1}{\partial X} \]
其中待估变量\( X = \begin{bmatrix} \alpha &\beta &\gamma &x &y &z \end{bmatrix}^T \)
以\(\alpha\)为例,推导Jacobian:
\[ \begin{aligned} \frac{\partial p_1}{\partial \alpha} &= \frac{\partial R}{\partial \alpha} \cdot s(p_2-st) \\[2mm] &=\frac{\partial \left(R_y(-\beta)*R_x(-\alpha)*R_z(-\gamma)\right)}{\partial \alpha} \cdot s(p_2-st) \\[2mm] &= \begin{pmatrix} -s\cos(\alpha s)*\sin(\beta s)*\sin(\gamma s) & s\cos(\alpha s)*\cos(\gamma s)*\sin(\beta s) & s\sin(\alpha s)*\sin(\beta s) \\ s\sin(\alpha s)*\sin(\gamma s) & -s\cos(\gamma s)*\sin(\alpha s) & s\cos(\alpha s) \\ s\cos(\alpha s)*\cos(\beta s)*\sin(\gamma s) & -s\cos(\alpha s)*\cos(\beta s)*\cos(\gamma s) & -s\cos(\beta s)*\sin(\alpha s) \end{pmatrix} \cdot s(p_2-st) \end{aligned} \]
可以看到,上面的公式跟Lidar Odometry文件里面的\(arx\)是完全吻合的。对\(\beta\)和\(\gamma\)的求导思路完全一样,这里略去。
float srx = sin(s * transform[0]);
float crx = cos(s * transform[0]);
float sry = sin(s * transform[1]);
float cry = cos(s * transform[1]);
float srz = sin(s * transform[2]);
float crz = cos(s * transform[2]);
float tx = s * transform[3];
float ty = s * transform[4];
float tz = s * transform[5];
float arx = (-s*crx*sry*srz*pointOri.x + s*crx*crz*sry*pointOri.y + s*srx*sry*pointOri.z
+ s*tx*crx*sry*srz - s*ty*crx*crz*sry - s*tz*srx*sry) * coeff.x
+ (s*srx*srz*pointOri.x - s*crz*srx*pointOri.y + s*crx*pointOri.z
+ s*ty*crz*srx - s*tz*crx - s*tx*srx*srz) * coeff.y
+ (s*crx*cry*srz*pointOri.x - s*crx*cry*crz*pointOri.y - s*cry*srx*pointOri.z
+ s*tz*cry*srx + s*ty*crx*cry*crz - s*tx*crx*cry*srz) * coeff.z;
论文中是优化轴角,而代码中是直接优化欧拉角。 按道理来说,每个点应该按照其所在的位置不同,将s设置为不同的比率,按照论文的思路也应该设置为不同的值。
而代码中将s始终设置为1,可能是因为对Lidar Odometry的精度要求不高?后面的Lidar Mapping会进一步优化坐标。
TODO:后面将进一步补充针对轴角做优化的公式。
接下来分析\(\partial d/\partial p_1\)的计算过程。
点线方程
假设点\(A(x_1,y_1)\)与点\(B(x_2,y_2)\)构成一条直线,求点\(O(x_0,y_0)\)到直线\(AB\)的距离,则:
\[ d=D(O,AB) \\[2mm] =\frac{\|OA\times OB\|}{\|AB\|} \\[2mm] \]
直接将上式进行代数展开,并以\(x\)为例,求其Jacobian矩阵如下:
(y1 - y2) #1 + (z1 - z2) #2
------------------------------------------------------------------
2 2 2 2 2 2
sqrt(#1 + #2 + #3 ) sqrt((x1 - x2) + (y1 - y2) + (z1 - z2) )
where:
#1 == (x0 - x1) (y0 - y2) - (x0 - x2) (y0 - y1)
#2 == (x0 - x1) (z0 - z2) - (x0 - x2) (z0 - z1)
#3 == (y0 - y1) (z0 - z2) - (y0 - y2) (z0 - z1)与代码也完全对应:
float a012 = sqrt(((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
* ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
+ ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
* ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
+ ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))
* ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)));
float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2));
float la = ((y1 - y2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
+ (z1 - z2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))) / a012 / l12;
点面方程
\[ d=D(O,ABC) \\[2mm] =\frac{(AB\times AC)\cdot OA}{\|AB \times AC\|} \\[2mm] \]
将数据进行代数展开,对点坐标求Jacobian,与代码也完全对应。
建图 #
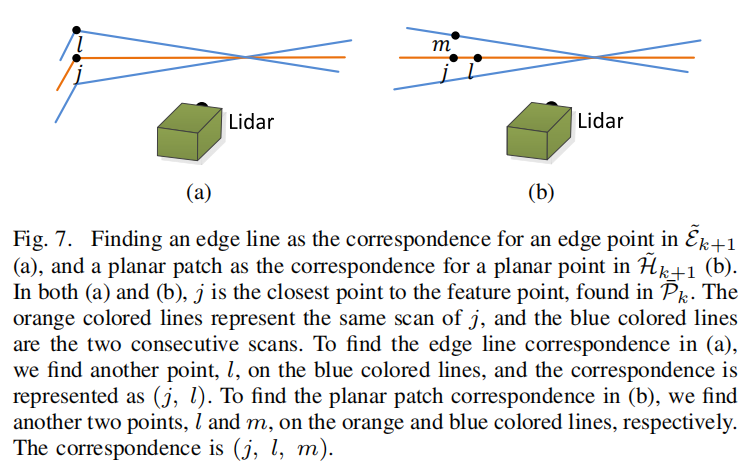
将地图中与当前帧有重叠的部分取出来,用KD-Tree保存。并进行滤波处理,减少计算量。 再寻找最邻近的5个点,对点云协方差矩阵进行主成分分析:
- 若这五个点分布在直线上,协方差矩阵的特征值包含一个元素显著大于其余两个,与该特征值相关的特征向量表示所处直线的方向;
- 若这五个点分布在平面上,协方差矩阵的特征值存在一个显著小的元素,与该特征值相关的特征向量表示所处平面的法线方向。
\[ d=D(p_w) \\[2mm] \begin{aligned} p_w &= R p_L + t \\[2mm] &=\left(R_y(\beta)*R_x(\alpha)*R_z(\gamma)\right) \cdot p_L + t \\[2mm] \end{aligned} \]
以\(\alpha\)为例,推导Jacobian:
\[ \begin{aligned} \frac{\partial p_w}{\partial \alpha} &= \frac{\partial R}{\partial \alpha} \cdot p_L \\[2mm] &=\frac{\partial \left(R_y(\beta)*R_x(\alpha)*R_z(\gamma)\right)}{\partial \alpha} \cdot p_L \\[2mm] &= \begin{pmatrix} \cos(\alpha)*\sin(\beta)*\sin(\gamma)& \cos(\alpha)*\cos(\gamma)*\sin(\beta)& -\sin(\alpha)*\sin(\beta) \\ -\sin(\alpha)*\sin(\gamma)& -\cos(\gamma)*\sin(\alpha)& -\cos(\alpha) \\ \cos(\alpha)*\cos(\beta)*\sin(\gamma)& \cos(\alpha)*\cos(\beta)*\cos(\gamma)& -\cos(\beta)*\sin(\alpha) \end{pmatrix} \cdot p_L \end{aligned} \]
优化过程与Lidar Odometry基本类似,不再赘述。
Next: ROS Integration
Previous: GNSS定位原理