Skip to main content

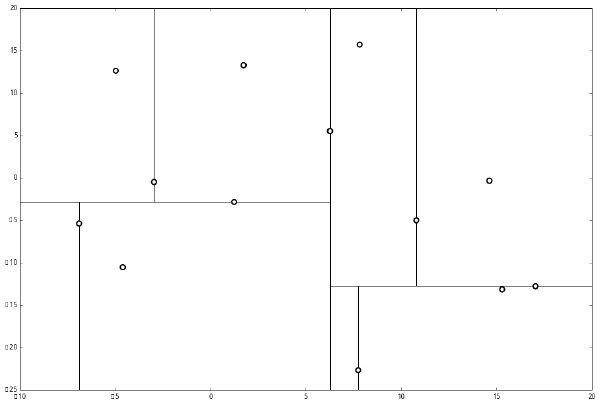
Kd Tree

Published: 2020-03-13

Table of contents
  1. 建立KD-Tree
  2. 查找元素
  3. 使用范例

建立KD-Tree #

  1. 选取方差最大的特征作为分割特征；
  2. 选择该特征的中位数作为分割点；
  3. 将数据集中该特征小于中位数的传递给根节点的左节点，大于中位数的传递给根节点的右节点；
  4. 递归执行步骤1-3，直到所有数据都被建立到KD Tree的节点上为止。
KD Tree

查找元素 #

  1. 从根节点开始，根据目标在分割特征中是否小于或大于当前节点，向左或向右移动；
  2. 一旦算法到达叶节点，它就将节点点保存为“当前最佳”；
  3. 回溯，即从叶节点再返回到根节点；
  4. 如果当前节点比当前最佳节点更接近，那么它就成为当前最好的；
  5. 如果目标距离当前节点的父节点所在的将数据集分割为两份的超平面的距离更接近，说明当前节点的兄弟节点所在的子树有可能包含更近的点。 因此需要对这个兄弟节点递归执行1-4步。

使用范例 #

AMCL 定位中，会使用大量的粒子描述状态的统计信息。为了防止最优粒子频繁切换带来的定位结果抖动，需要对粒子进行分组。 将临近的粒子分为一组，就需要使用KD-Tree进行查找。请参考 粒子聚类。

建立KD-Tree时，不一定要选择方差最大的特征作为分割特征，也不一定要选择该特征的中位数作为分割点。 进行这两个步骤的统计可能会消耗大量的计算，因此实际实现中，也可以随机选择某个数作为分割点。


Next: move_base 模块
Previous: RANSAC