GMapping

Published: 2020-01-08 | Lastmod: 2020-02-10

基本理论 #

粒子滤波基本原理请参考 Particle Filter

SLAM问题的分解

\[ \begin{aligned} p(x_{1:t},m|u_{1:t},z_{1:t}) &= p(x_{1:t}|u_{1:t},z_{1:t}) p(m|u_{1:t},z_{1:t})\\ &= p(x_{1:t}|u_{1:t},z_{1:t}) p(m|z_{1:t}) \end{aligned} \]

将SLAM问题分解为：机器人的定位；基于已知机器人位姿的构图。

Fast-SLAM

根据贝叶斯公式，可以将机器人位姿的估计，转换成一个增量估计问题。

\[ \begin{aligned} p(x_{1:t}|u_{1:t},z_{1:t}) &= \eta p(z_t|x_{1:t},u_{1:t},z_{1:t-1}) p(x_{1:t}|z_{1:t-1},u_{1,t})\\ &= \eta p(z_t|x_t) p(x_{1:t}|z_{1:t-1},u_{1:t})\\ &= \eta p(z_t|x_t) p(x_t|x_{1:t-1},z_{1:t-1},u_{1:t}) p(x_{1:t-1}|z_{1:t-1},u_{1:t})\\ &= \eta p(z_t|x_t) p(x_t|x_{t-1},u_{1:t}) p(x_{1:t-1}|z_{1:t-1},u_{1:t-1}) \end{aligned} \]

其中，\(p(x_{1:t-1}|z_{1:t-1},u_{1:t-1})\)通过粒子群来表示； \(p(x_t|x_{t-1},u_{1:t})\)对每个粒子进行运动学模型的传播； \(p(z_t|x_t)\)根据观测模型计算权重。

数据结构相关 #

Map

template <class Cell, const bool debug=false> class Array2D{};
template <class Cell> class HierarchicalArray2D: public Array2D<autoptr< Array2D<Cell> > >{};
template <class Cell, class Storage, const bool isClass=true> class Map{};
typedef Map<PointAccumulator,HierarchicalArray2D<PointAccumulator> > ScanMatcherMap;

Array2D是一个二维数组，HierarchicalArray2D是一个Array2D的二维数组。 相当于将地图先分割成分辨率比较低的网格，只有当粒子运动到该网格时，才真正分配这个网格的内存。 网格的内存对应着分辨率高的真实的地图，用PointAccumulator来进行计数，记录激光是否通过该点，从而判断改点的状态：占据、空闲、未知。

autoptr

GMapping中自己实现了autoptr类，实现了智能指针的功能。

运动更新 #

根据上一时刻的状态，结合里程计的输入量，可以得到当前时刻预估的状态。

\[ x_t = g_t(u_t, x_{t-1}) + \varepsilon_t \]

权重计算 #

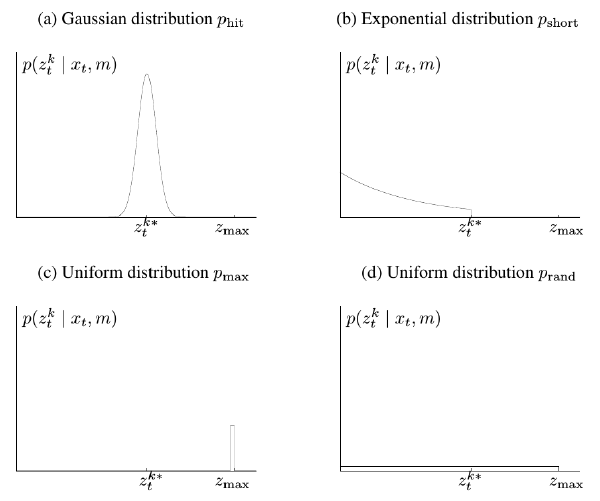
光束模型

使用Bresenham画线算法，进行高效的计算。 由于计算量过大、在非结构化环境中得分会突变，因此实际工程项目中很少采用此方法。

\[ p(z_t^k|x_t,m)=\begin{pmatrix} z_{hit} \\ z_{short} \\ z_{max} \\ z_{rand} \end{pmatrix}^T \begin{pmatrix} p_{hit}(z_t^k|x_t,m) \\ p_{short}(z_t^k|x_t,m) \\ p_{max}(z_t^k|x_t,m) \\ p_{rand}(z_t^k|x_t,m) \end{pmatrix} \]

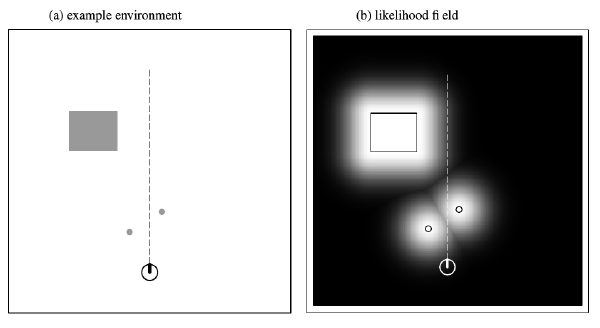
似然场模型

对图像进行高斯平滑，不会出现得分突变的情况，且运算效率高，查表即可得到。是工程项目中常用的方法。

重采样优化 #

里程计扩散出来的最好的粒子

若里程计信号质量误差较大，则需要大量粒子对验后分布进行模拟。由于每个粒子都携带一个地图，这将会造成巨大的内存消耗。 根据里程计的运动模型，每个粒子会扩散出很多粒子。从其中找出最好的那个粒子，其他的全去除，可以大量减少粒子数量。

\[ x_t^i \sim p(x_t|u_t,x_{t-1}^i) \\[2mm] \to x_t^i = \arg \max_{x_t}(p(z_t|x_t,m)p(x_t|u_t,x_{t-1}^i)) \]

抑制重采样次数

当采样次数过多时，会出现粒子耗散问题，即所有的粒子来自于少数几个粒子。

\[ N_{eff} = \frac{1}{\sum_{i = 1}^N \left(\tilde{w}^{(i)} \right)^2} \]

当\(N_{eff}\)较大时，说明各粒子的差异性较小，此时不要进行重采样。反之，则应进行重采样。

根据激光匹配估计出分布

由于激光的精度较高，可以通过激光的匹配，估计出一个高斯分布。并在此分布中进行采样，得到一系列粒子。

建图算法 #

覆盖栅格建图

\[ l(m_i|x_{1:t},z_{1:t})=l(m_i|x_t,z_t)+l(m_i|x_{1:t-1},z_{1:t-1})-l(m_i) \]

其中，\(l(m_i|x_t,z_t)\)表示会激光雷达的逆观测模型；\(l(m_i|x_{1:t-1},z_{1:t-1})\)表示栅格\(m_i\)在\(t-1\)时刻的状态， \(l(m_i)\)表示栅格\(m_i\)的先验值，对所有栅格都相同。

计数建图法

\[ m_j = \frac{a_j}{a_j+b_j} \]

其中，\(a_j\)表示击中的次数，\(b_j\)表示未击中的次数。