Bayesian Filter

Published: 2020-02-10 | Lastmod: 2020-04-03

Kalman Filter #

Imagine you are in a car equipped with sensors on the outside. The car sensors can detect objects moving around: for example, the sensors might detect a pedestrian, as described in the video, or even a bicycle. For variety, let's step through the Kalman Filter algorithm using the bicycle example.

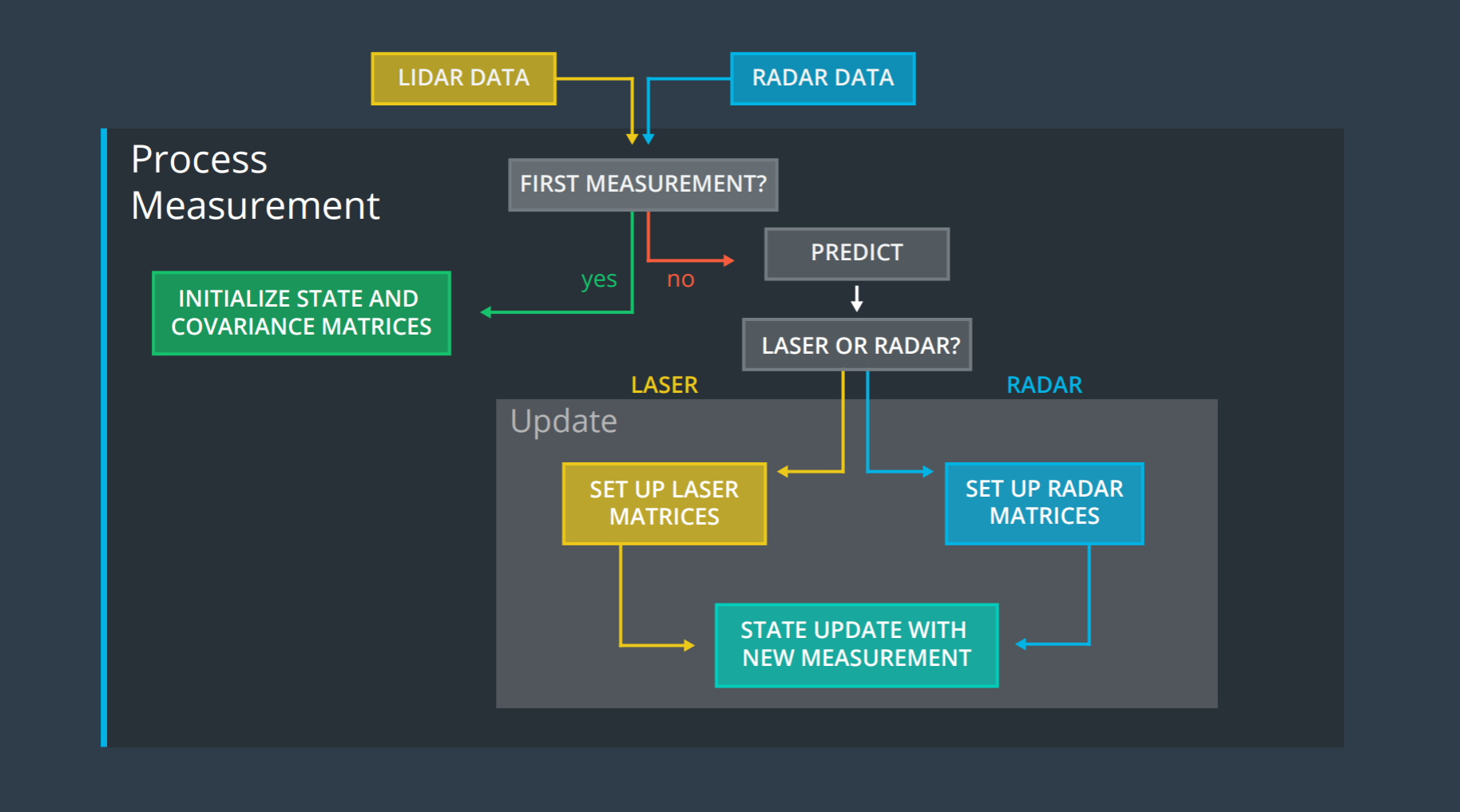
The Kalman Filter algorithm will go through the following steps:

1. first measurement - the filter will receive initial measurements of the bicycle's position relative to the car. These measurements will come from a radar or lidar sensor.
2. initialize state and covariance matrices - the filter will initialize the bicycle's position based on the first measurement.
3. then the car will receive another sensor measurement after a time period \(\Delta t\).
4. predict - the algorithm will predict where the bicycle will be after time \(\Delta t\). One basic way to predict the bicycle location after \(\Delta t\) is to assume the bicycle's velocity is constant; thus the bicycle will have moved velocity * \(\Delta t\). In the extended Kalman filter lesson, we will assume the velocity is constant.
5. update - the filter compares the "predicted" location with what the sensor measurement says. The predicted location and the measured location are combined to give an updated location. The Kalman filter will put more weight on either the predicted location or the measured location depending on the uncertainty of each value.
6. then the car will receive another sensor measurement after a time period \(\Delta t\). The algorithm then does another predict and update step.

Extended Kalman Filter (EKF)

动态方程

常速度模型下，加速度为白噪声。

\[ \begin{pmatrix} p'_x \\ p'_y \\ v'_x \\ v'_y \end{pmatrix} = \underbrace{\begin{pmatrix} 1 &0 &\Delta t &0 \\ 0 &1 &0 &\Delta t \\ 0 &0 &1 &0 \\ 0 &0 &0 &1 \end{pmatrix}}_F \begin{pmatrix} p_x \\ p_y \\ v_x \\ v_y \end{pmatrix} + \begin{pmatrix} \frac{a_x \Delta t^2}{2} \\ \frac{a_y \Delta t^2}{2} \\ a_x \Delta t \\ a_y \Delta t \end{pmatrix} \]

其中动态噪声的协方差矩阵，应该根据与加速度白噪声的关系确定。而加速度的白噪声大小属于先验值。

\[ \begin{pmatrix} \frac{a_x \Delta t^2}{2} \\ \frac{a_y \Delta t^2}{2} \\ a_x \Delta t \\ a_y \Delta t \end{pmatrix} = \underbrace{\begin{pmatrix} \frac{\Delta t^2}{2} &0 \\ 0 &\frac{\Delta t^2}{2} \\ \Delta t &0 \\ 0 &\Delta t \end{pmatrix}}_G \begin{pmatrix} a_x \\ a_y \end{pmatrix} \]

根据协方差传播定律，在已知\(a_x\)、\(a_y\)的标准差为\(\sigma_{ax}\)、\(\sigma_{ay}\)的情况下，动态噪声的协方差矩阵为：

\[ Q = GQ_vG^T= \begin{pmatrix} \frac{\Delta t^2}{2} &0 \\ 0 &\frac{\Delta t^2}{2} \\ \Delta t &0 \\ 0 &\Delta t \end{pmatrix} \begin{pmatrix} \sigma_{ax}^2 &0 \\ 0 &\sigma_{ay}^2 \end{pmatrix} \begin{pmatrix} \frac{\Delta t^2}{2} &0 &\Delta t &0 \\ 0 &\frac{\Delta t^2}{2} &0 &\Delta t \end{pmatrix} \]

Lidar

\[ \begin{pmatrix} p_x \\ p_y \end{pmatrix} = \underbrace{\begin{pmatrix} 1 &0 &0 &0 \\ 0 &1 &0 &0 \end{pmatrix}}_H \begin{pmatrix} p'_x \\ p'_y \\ v'_x \\ v'_y \end{pmatrix} \]

观测值的噪声为先验值：

\[ R=\begin{pmatrix} \sigma_{px}^2 &0 \\ 0 &\sigma_{py}^2 \end{pmatrix} \]

Radar

\[ \begin{aligned} \begin{pmatrix} \rho \\ \phi \\ \dot{\rho} \end{pmatrix} &= \begin{pmatrix} \sqrt{{p'_x}^2+{p'_y}^2} \\ \arctan(p'_y / p'_x) \\ \frac{p'_x v'_x + p'_y v'_y}{\sqrt{{p'_x}^2+{p'_y}^2}} \end{pmatrix} \\[2mm] &\approx \begin{pmatrix} \sqrt{p_x^2+p_y^2} \\ \arctan(p_y / p_x) \\ \frac{p_x v_x + p_y v_y}{\sqrt{p_x^2+p_y^2}} \end{pmatrix} + \underbrace{\begin{pmatrix} \frac{p_x}{\sqrt{p_x^2+p_y^2}} &\frac{p_y}{\sqrt{p_x^2+p_y^2}} &0 &0 \\ -\frac{p_y}{p_x^2+p_y^2} &\frac{p_x}{p_x^2+p_y^2} &0 &0 \\ \frac{p_y(v_xp_y-v_yp_x)}{(p_x^2+p_y^2)^{3/2}} &\frac{p_x(v_yp_x-v_xp_y)}{(p_x^2+p_y^2)^{3/2}} &\frac{p_x}{\sqrt{p_x^2+p_y^2}} &\frac{p_y}{\sqrt{p_x^2+p_y^2}} \end{pmatrix}}_{H_j} \begin{pmatrix} p'_x - p_x \\ p'_y - p_y \\ v'_x - v_x \\ v'_y - v_y \end{pmatrix} \end{aligned} \]

观测值的噪声为先验值：

\[ R=\begin{pmatrix} \sigma_{\rho}^2 &0 &0 \\ 0 &\sigma_{\phi}^2 &0 \\ 0 &0 &\sigma_{\dot{\rho}}^2 \end{pmatrix} \]

已知状态转移矩阵\(F\)、动态噪声\(Q\)，便可以预测下一时刻的状态和协方差；
已知观测矩阵\(H\)、观测噪声\(R\)，当更新一个观测量\(z\)时，便可以得到最优估计状态和协方差。

Error State Extended Kalman Filter (ES-EKF)

参考 An Improved EKF - The Error State Extended Kalman Filter

More

迭代卡尔曼：当非线性化程度高的时候，可能需要迭代多次。每次迭代时候，协方差\(P\)要保持相同不变，只更新先验的状态量\(x\)。

最小二乘：当迭代多次，且动态噪声设置为无穷大时，观测噪声起主导作用，其效果等同于最小二乘。

序列化卡尔曼滤波：将观测量依次输入，矩阵运算变为标量运算，减小计算量，同时可以剔除粗差。

Unscented Kalman Filter #

CVTR

CVTR表示运动模型为常速度、常转向角速度，其微分方程可以写做：

\[ \begin{pmatrix} \dot{p_x} \\ \dot{p_y} \\ \dot{v} \\ \dot{\psi} \\ \ddot{\psi} \end{pmatrix} = \begin{pmatrix} v\cdot\cos(\psi) \\ v\cdot\sin(\psi) \\ 0 \\ \dot{\psi} \\ 0 \end{pmatrix} \]

对上式进行积分，可得：

\[ \begin{aligned} x_{k+1} &= x_k + \int_{t_k}^{t_{k+1}} \begin{pmatrix} \dot{p_x}(t) \\ \dot{p_x}(t) \\ \dot{v}(t) \\ \dot{\psi}(t) \\ \ddot{\psi}(t) \end{pmatrix} dt + \nu \\[2mm] &=x_k+ \begin{pmatrix} v_k\int_{t_k}^{t_{k+1}}\cos(\psi_k+\dot{\psi}_k\cdot(t-t_k))dt \\ v_k\int_{t_k}^{t_{k+1}}\cos(\psi_k+\dot{\psi}_k\cdot(t-t_k))dt \\ 0 \\ \dot{\psi}_k\Delta t \\ 0 \end{pmatrix} + \nu \\[2mm] &=x_k+ \begin{pmatrix} \frac{v_k}{\dot{\psi}_k}\left(\sin(\psi_k+\dot{\psi}_k\Delta t)-\sin(\psi_k)\right) \\ \frac{v_k}{\dot{\psi}_k}\left(-\cos(\psi_k+\dot{\psi}_k\Delta t)+\cos(\psi_k)\right) \\ 0 \\ \dot{\psi}_k\Delta t \\ 0 \end{pmatrix} + \begin{pmatrix} \frac{1}{2}(\Delta t)^2\cos(\psi_k)\cdot\nu_{a,k} \\ \frac{1}{2}(\Delta t)^2\sin(\psi_k)\cdot\nu_{a,k} \\ \Delta t\cdot\nu_{a,k} \\ \frac{1}{2}(\Delta t)^2\cdot\nu_{\ddot{\psi},k} \\ \Delta t\cdot\nu_{\ddot{\psi},k} \end{pmatrix} \text{ if } \dot{\psi}\neq0 \\[2mm] &=x_k+ \begin{pmatrix} v_k\cos\psi_k\Delta t \\ v_k\sin\psi_k\Delta \\ 0 \\ 0 \\0 \end{pmatrix} + \begin{pmatrix} \frac{1}{2}(\Delta t)^2\cos(\psi_k)\cdot\nu_{a,k} \\ \frac{1}{2}(\Delta t)^2\sin(\psi_k)\cdot\nu_{a,k} \\ \Delta t\cdot\nu_{a,k} \\ \frac{1}{2}(\Delta t)^2\cdot\nu_{\ddot{\psi},k} \\ \Delta t\cdot\nu_{\ddot{\psi},k} \end{pmatrix} \text{ if } \dot{\psi}=0 \end{aligned} \]

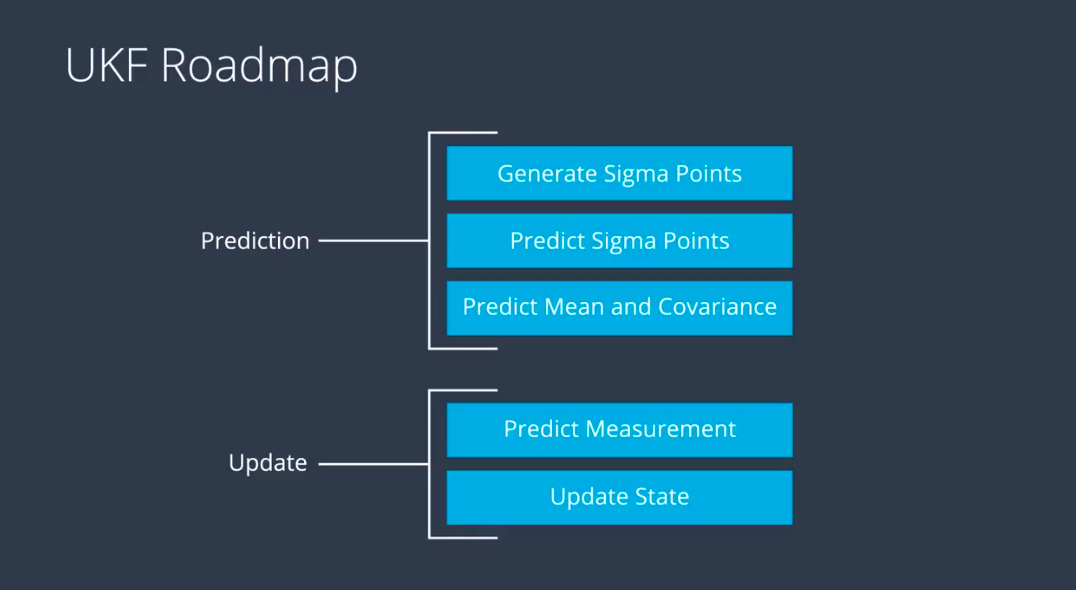
UKF

对于动态方程高度非线性化，可以使用UKF进行参数估计。其核心思想为，按照高斯分布采样点，通过非线性函数后，对变化后的点进行高斯分布拟合。

Generate Sigma Points

\[ X_{k|k} = \begin{pmatrix} x_{k|k} & x_{k|k}+\sqrt{(\lambda+n_x)P_{k|k}} & x_{k|k}-\sqrt{(\lambda+n_x)P_{k|k}} \end{pmatrix} \]

with scaling factor \(\lambda=3-n_x\)

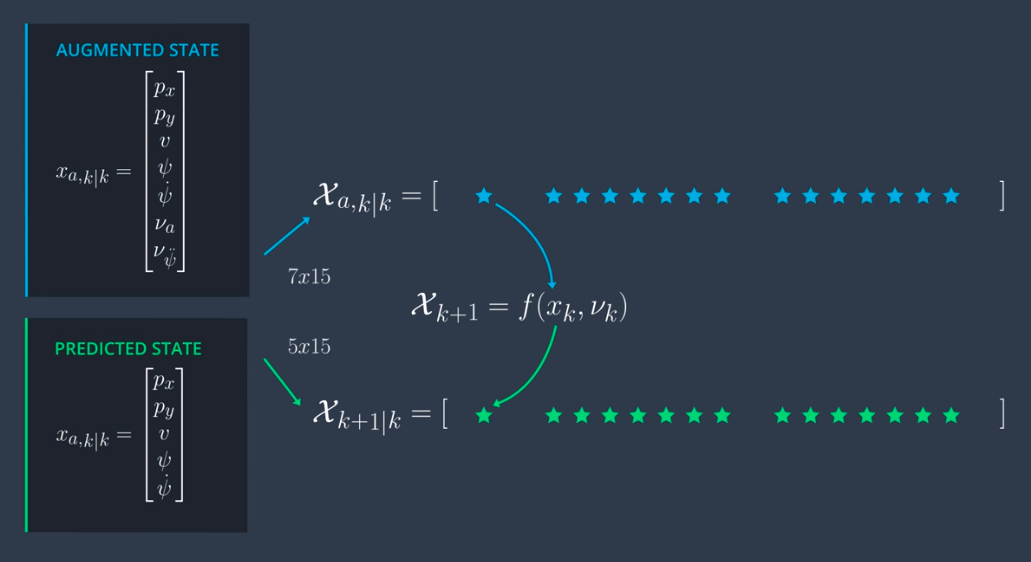
为了将动态噪声的影响纳入，需要采用状态增广的方法：

Predict Sigma Points

使用上面推导的CVTR模型，预测Sigma Points。

Predict Mean and Covariance

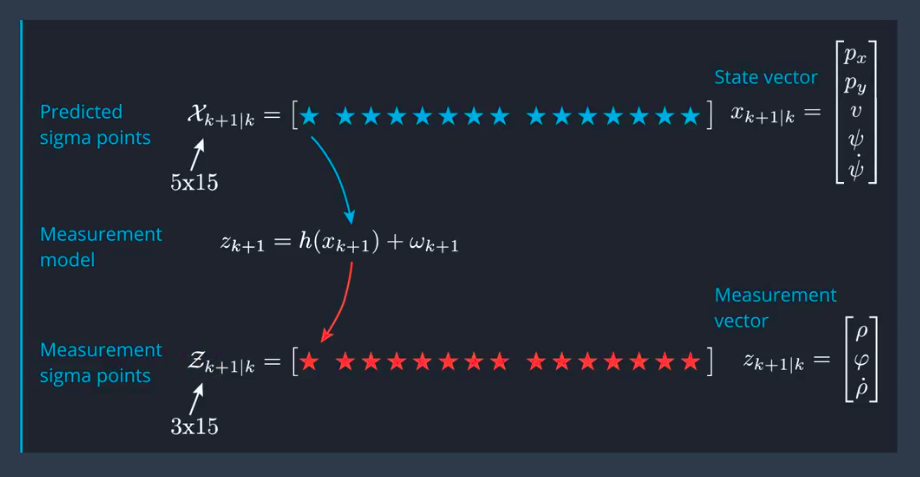
Measurement Prediction

由于观测噪声是可直接相加，因此不再需要状态增广。

UKF Update

Here you need the cross-correlation matrix between the predicted sigma points in the state space and the predicted sigma points in the measurement space.

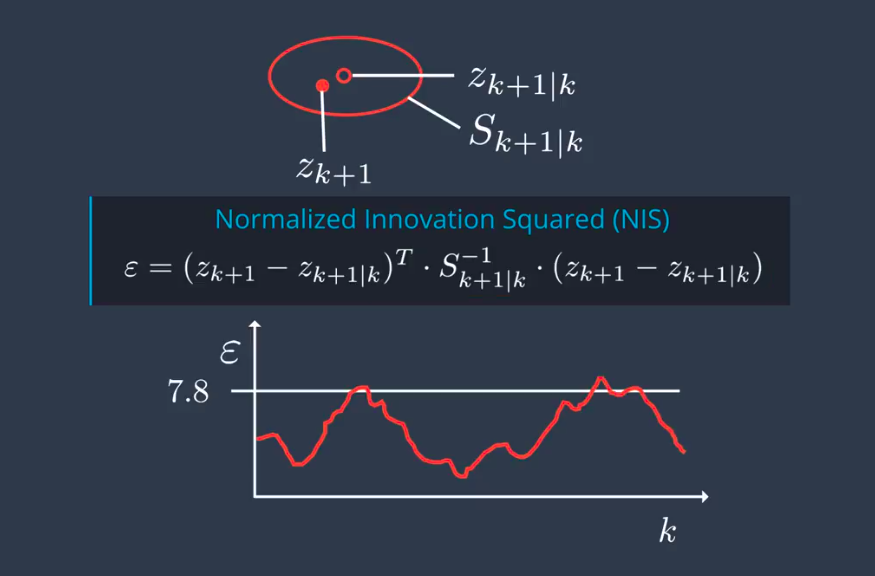
Parameters And Consistency

服从\(\chi^2\)分布，对于Radar传感器，有3个观测量，自由度为3。查表可知，统计上来说，5%的NIS值会超过7.8。

Partical Filter #

Init

在初始点附近生成N个粒子。

for (int i = 0; i < num_particles; ++i) {
    Particle p;
    p.id = i;
    p.weight = 1.0;
    p.x	= dist_x(gen);
    p.y	= dist_y(gen);
    p.theta	= dist_theta(gen);
    particles.push_back(p);
}

Prediction

根据Motion Model，预测下一时刻位置，并添加动态噪声。

if (fabs(yaw_rate) > 1e-5) {
    theta_new = theta_old + yaw_rate * delta_t;
    x_new = x_old + velocity / yaw_rate * (sin(theta_new) - sin(theta_old));
    y_new = y_old + velocity / yaw_rate * (cos(theta_old) - cos(theta_new));
} else {
    theta_new = theta_old;
    x_new = x_old + velocity * delta_t * cos(theta_old);
    y_new = y_old + velocity * delta_t * sin(theta_old);
}

normal_distribution<double> dist_x(x_new, std_pos[0]);
normal_distribution<double> dist_y(y_new, std_pos[1]);
normal_distribution<double> dist_theta(theta_new, std_pos[2]);

particle.x = dist_x(gen);
particle.y = dist_y(gen);
particle.theta = dist_theta(gen);

DataAssociation

根据观测值，找到地图上对应的点。

for (auto& observation : observations) {
    double min_dist = 9999.0;
    for (auto& predict : predicted) {
        double d = dist(observation.x, observation.y, predict.x, predict.y);
        if (d < min_dist) {
            observation.id = predict.id;
            min_dist = d;
        }
    }
}

Update Weight

把观测的点，与找到的地图上的点，求正态分布概率。

for (auto& obs : observations_map) {
    for (auto& land: visibleLandmarks_map)
        if (obs.id == land.id) {
            mu_x = land.x;
            mu_y = land.y;
            break;
        }
    double tmp = exp( -( pow(obs.x - mu_x, 2) / (2 * std_landmark[0] * std_landmark[0]) 
               + pow(obs.y - mu_y, 2) / (2 * std_landmark[1]* std_landmark[1]) ) ) 
               / (2 * M_PI * std_landmark[0]* std_landmark[1]);
    if(fabs(tmp) < 1e-15) continue;
    particle_likelihood *= tmp;
}
particle.weight = particle_likelihood;

之后对粒子的概率进行归一化。

for (auto& particle : particles)
    particle.weight /= weights_sum;

Resample

根据权值重采样，权值大的容易被多次采到，表示该粒子所在的位置更接近真实值，粒子在此处渐渐聚集。 重采样之后，每个粒子的权值重新赋值为1。

vector<double> particle_weights;
for (auto& particle : particles)
    particle_weights.push_back(particle.weight);

discrete_distribution<int> weighted_distribution(particle_weights.begin(), particle_weights.end());

vector<Particle> resampled_particles;
default_random_engine gen;
for (int i = 0; i < num_particles; ++i) {
    int k = weighted_distribution(gen);
    particles[k].weight = 1.0;
    resampled_particles.push_back(particles[k]);
}

particles = resampled_particles;

多余的话 #

动态方程的确定：

1. 直接写出下一时刻状态量\(x_{k+1}\)与当前时刻状态量\(x_k\)的数学方程；（本文中的EKF）
2. 直接写出状态量导数\(\dot{x}\)与状态量\(x\)的数学方程；
   • 积分得到下一时刻状态量\(x_{k+1}\)与当前时刻状态量\(x_k\)的数学方程；（本文中的UKF / VINS-MONO的代码实现）
   • 求得error-state状态方程，即\(\dot{\delta x}\)与\(\delta x\)的数学方程；（MSCKF / GPS&INS组合导航 / VINS-MONO论文）