Skip to main content

AMCL

Published: 2020-01-02 | Lastmod: 2020-02-10

Table of contents
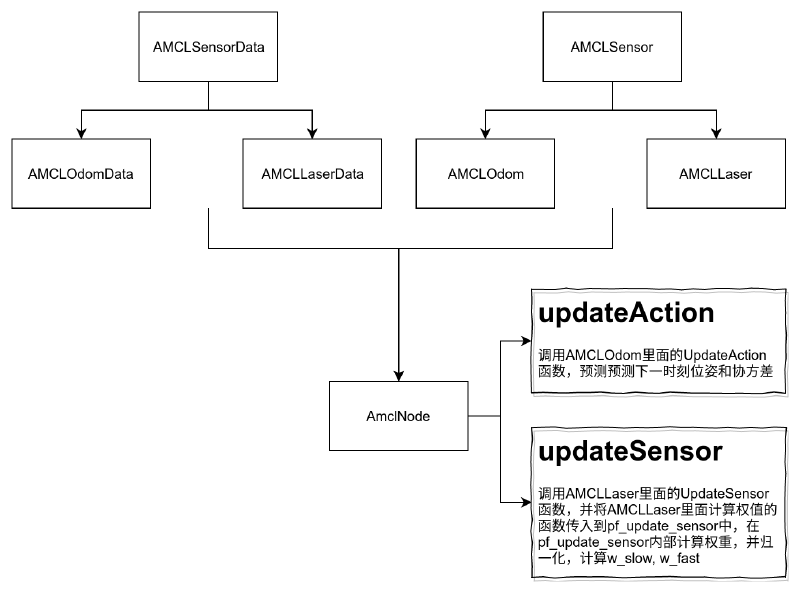
  1. ROS-AMCL
  2. 粒子聚类
  3. 粒子滤波改进
  4. 距离计算
  5. AMCL参数解读
  6. 参考资料

ROS-AMCL #

AMCL

粒子滤波基本原理请参考 Particle Filter

粒子聚类 #

对外输出的机器人状态不应该是某一个最好的粒子，因为很有可能某些粒子的值都非常接近，可能会引起频繁的粒子切换，导致输出的结果来回跳变。

基于此考虑， 应该对相似的粒子进行聚类。将最好的那一簇粒子的统计状态作为输出的机器人状态。

KD-Tree

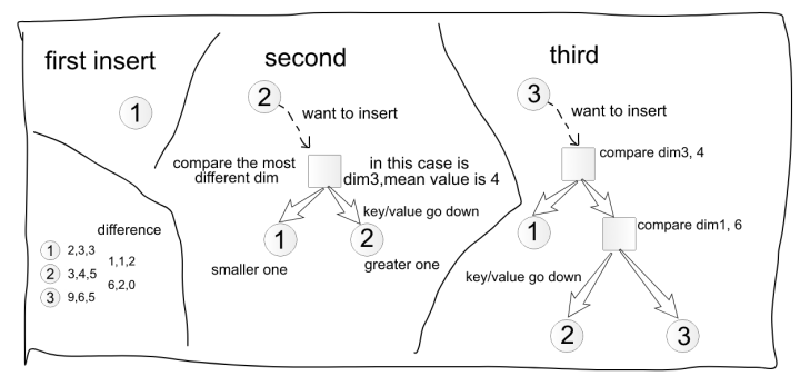
当涉及到距离查找时，作为算法工程师，我们应该首先想到KD-Tree。树的叶子节点是每一个粒子，而非叶子节点则保存的是该节点的分叉判断的标准，小于此分叉判断标准的在左边，大于此分叉标准的在右边。

查询的基本思路：首先通过二叉树搜索（比较待查询节点和分裂节点的分裂维的值，小于等于就进入左子树分支，等于就进入右子树分支直到叶子结点），顺着“搜索路径”很快能找到最近邻的近似点，也就是与待查询点处于同一个子空间的叶子结点；然后再回溯搜索路径，并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他子结点空间中去搜索（将其他子结点加入到搜索路径）。重复这个过程直到搜索路径为空。

KD-Tree

聚类

循环遍历每一个叶子节点，在叶子节点周围的 +-1 范围内的粒子都归为一类。例如在AMCL中，每个粒子周围27个粒子若有相连的，就将它们全部连成一片，形成一簇粒子。

粒子滤波改进 #

为了防止机器人被绑架，出现粒子收敛于某一错误的地方，需要进行粒子滤波的改良。

粒子注入

我们来考虑如下的式子：

\[ x_1 = x + 0.1(y-x) \\[2mm] x_2 = x + 0.9(y-x) \]

对于上面两个式子，展开以后我们可以发现：\(x_1\) 主要受到 \(x\) 的影响，而 \(x_2\) 主要受到 \(y\) 的影响。若粒子收敛于正确的状态，则 \(y\) 是准确的，\(x_2\) 将会比 \(x_1\) 更大，此时不需要注入粒子。若粒子收敛于错误的地方，则 \(y\) 不准确，此时 \(x_1\) 受到 \(y\) 的影响较小，\(x_1\) 更准确，此时便需要注入粒子。

而这正是AMCL里面slow和fast参数产生的效果。

KLD自适应

KLD的计算属于数理统计的知识，可参考论文1。这里进行直观的解释。

例如，某一粒子权值很大。当我们进行100次采样，可能都采样到的是同一个粒子，此时粒子的个数始终保持为1。而KLD计算出来的需要采样的次数，是粒子个数的函数。因此，当粒子数保持为1时，KLD计算出来的次数为某一定值，而采样次数持续在增加，到某一时间点，便超过了需要的采样次数。

而当粒子权值都接近时，假设我们采样了100次，每次采样出来的粒子都不同，此时粒子的个数一直增长到100。此时的KLD也随着粒子的个数增长到一个比较大的值。采样的次数虽然持续增加，但是始终超过不了KDL计算出来的次数。此种情况下采样仍将继续。

距离计算 #

计算每个粒子的权重时，我们需要计算观测到的障碍物与地图中的障碍物的距离差异。差异越大，权值越小。当某次观测的障碍物全部与地图上的障碍物匹配上了，则差异为0，权值极大。因此，在地图的初始阶段，我们需要计算地图上任一点位置到最近障碍物的距离。这就是似然场模型。

直接计算

遍历每一个点，计算每一个点到每个障碍物的距离并取最小值。此方法进行了重复计算，效率较低。

高效算法

从障碍物出发，向外膨胀一个单位。当所有障碍物膨胀完以后，从膨胀出来的地方出发，继续向外膨胀一个单位。此方法没有冗余计算，且实现的代码简洁。

AMCL参数解读 #

min_particles / max_particles / kld_err / kld_z : 用来限制粒子数量
update_min_d / update_min_a / resample_interval : 限制冲采样条件
recovery_alpha_slow / recovery_alpha_fast : 动态调整粒子数量
initial_pose_xya / initial_cov_xxyyaa : 初始位置及其协方差
odom_alpha1234 : 里程计运动模型误差系数

参考资料 #

http://www.robots.ox.ac.uk/~cvrg/hilary2005/adaptive.pdf
https://blog.csdn.net/Mark_SLAM/article/details/81266527
https://zhuanlan.zhihu.com/p/28137335
https://zhuanlan.zhihu.com/p/59411695
https://zhuanlan.zhihu.com/p/59663340
https://zhuanlan.zhihu.com/p/61908381
udacity robot
github particle filter


Next: MSCKF
Previous: Hugo搭建网站